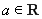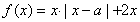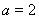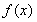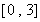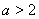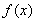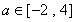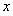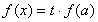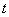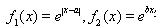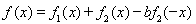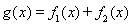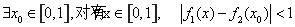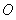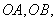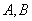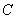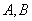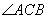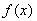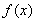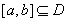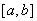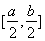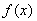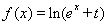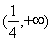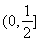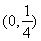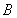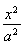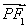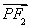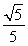题目内容
已知二次函数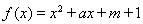 ,关于x的不等式
,关于x的不等式 的解集为
的解集为 ,其中m为非零常数.设
,其中m为非零常数.设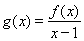 .
.
(1)求a的值;
(2)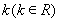 如何取值时,函数
如何取值时,函数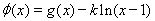 存在极值点,并求出极值点;
存在极值点,并求出极值点;
(3)若m=1,且x>0,求证: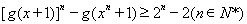
(1)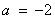 (2)当
(2)当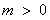 时,
时,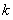 取任何实数, 函数
取任何实数, 函数 有极小值点
有极小值点 ;
;
当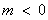 时,
时,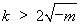 ,函数
,函数 有极小值点
有极小值点 ,有极大值点
,有极大值点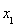 .…9分
.…9分
(其中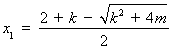 ,
, 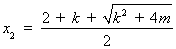 )(3)见解析
)(3)见解析
【解析】(1)【解析】
∵关于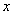 的不等式
的不等式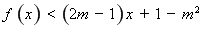 的解集为
的解集为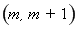 ,
,
即不等式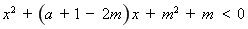 的解集为
的解集为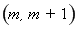 ,
,
∴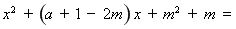
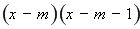 .
.
∴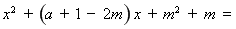
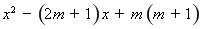 .
.
∴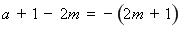 .
.
∴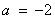 .
.
(2)解法1:由(1)得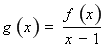
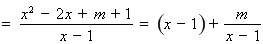 .
.
∴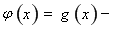
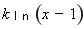
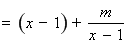
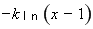 的定义域为
的定义域为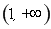 .
.
∴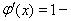
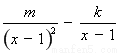
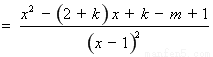 . ………3分
. ………3分
方程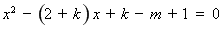 (*)的判别式
(*)的判别式
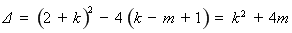 .………4分
.………4分
①当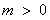 时,
时,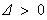 ,方程(*)的两个实根为
,方程(*)的两个实根为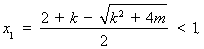
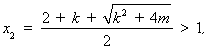 ………5分
………5分
则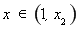 时,
时,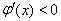 ;
;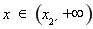 时,
时,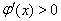 .
.
∴函数 在
在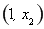 上单调递减,在
上单调递减,在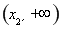 上单调递增.
上单调递增.
∴函数 有极小值点
有极小值点 . ………6分
. ………6分
②当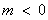 时,由
时,由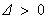 ,得
,得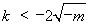 或
或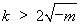 ,
,
若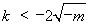 ,则
,则
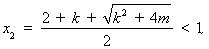
故
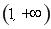 时,
时,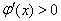 ,
,
∴函数 在
在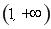 上单调递增.
上单调递增.
∴函数 没有极值点.………7分
没有极值点.………7分
若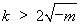 时,
时,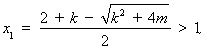
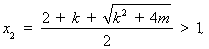
则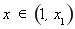 时,
时,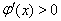 ;
;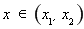 时,
时,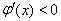 ;
;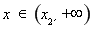 时,
时,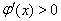 .
.
∴函数 在
在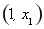 上单调递增,在
上单调递增,在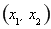 上单调递减,在
上单调递减,在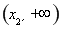 上单调递增.
上单调递增.
∴函数 有极小值点
有极小值点 ,有极大值点
,有极大值点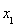 . ………8分
. ………8分
综上所述, 当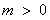 时,
时,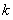 取任意实数, 函数
取任意实数, 函数 有极小值点
有极小值点 ;
;
当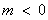 时,
时,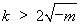 ,函数
,函数 有极小值点
有极小值点 ,有极大值点
,有极大值点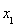 .…9分
.…9分
(其中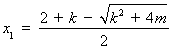 ,
, 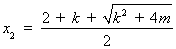 )
)
解法2:由(1)得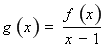
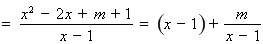 .
.
∴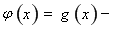
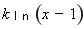
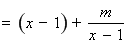
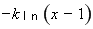 的定义域为
的定义域为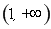 .
.
∴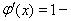
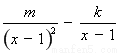
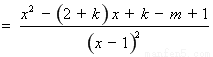 . ………3分
. ………3分
若函数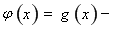
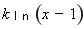 存在极值点等价于函数
存在极值点等价于函数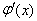 有两个不等的零点,且
有两个不等的零点,且
至少有一个零点在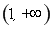 上. ………4分
上. ………4分
令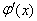
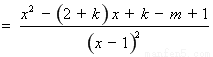
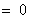 ,
,
得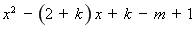
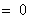 , (*)
, (*)
则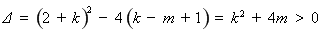 ,(**)…………5分
,(**)…………5分
方程(*)的两个实根为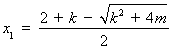 ,
, 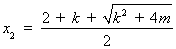 .
.
设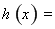
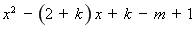 ,
,
①若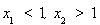 ,则
,则 ,得
,得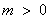 ,此时,
,此时,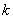 取任意实数, (**)成立.
取任意实数, (**)成立.
则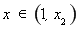 时,
时,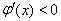 ;
;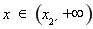 时,
时,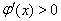 .
.
∴函数 在
在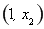 上单调递减,在
上单调递减,在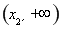 上单调递增.
上单调递增.
∴函数 有极小值点
有极小值点 . ………6分
. ………6分
②若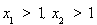 ,则
,则 得
得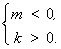
又由(**)解得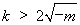 或
或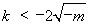 ,
,
故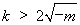 .………7分
.………7分
则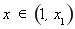 时,
时,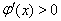 ;
;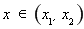 时,
时,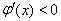 ;
;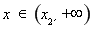 时,
时,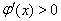 .
.
∴函数 在
在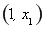 上单调递增,在
上单调递增,在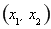 上单调递减,在
上单调递减,在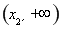 上单调递增.
上单调递增.
∴函数 有极小值点
有极小值点 ,有极大值点
,有极大值点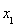 . ………8分
. ………8分
综上所述, 当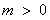 时,
时,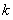 取任何实数, 函数
取任何实数, 函数 有极小值点
有极小值点 ;
;
当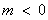 时,
时,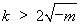 ,函数
,函数 有极小值点
有极小值点 ,有极大值点
,有极大值点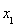 .…9分
.…9分
(其中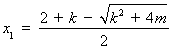 ,
, 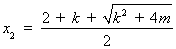 )
)
(3)∵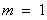 , ∴
, ∴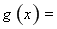
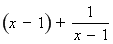 .
.
∴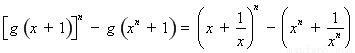
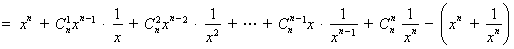
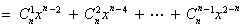 . ………10分
. ………10分
令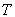
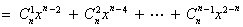 ,
,
则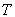

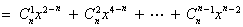 .
.
∵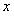
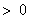 ,
,
∴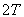
 …11分
…11分
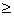
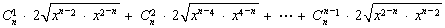 12分
12分
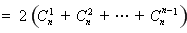

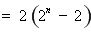 .………13分
.………13分
∴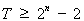 ,即
,即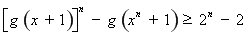 . ……………14分
. ……………14分
证法2:下面用数学归纳法证明不等式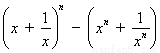
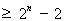 .
.
① 当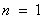 时,左边
时,左边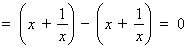 ,右边
,右边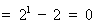 ,不等式成立;
,不等式成立;
………10分
②假设当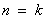
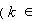 N
N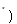 时,不等式成立,即
时,不等式成立,即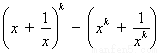
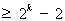 ,
,
则 
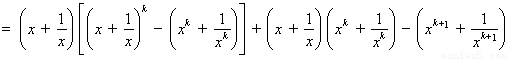
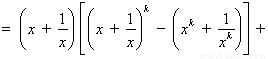
 ………11分
………11分
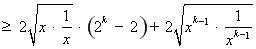 ………12分
………12分
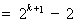 . ………13分
. ………13分
也就是说,当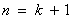 时,不等式也成立.
时,不等式也成立.
由①②可得,对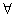
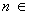 N
N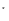 ,
,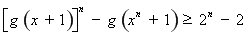 都成立. …14分
都成立. …14分