Question

【题目】已知在△ABC中，A=450，AB=，BC=2，求解此三角形.

Answer 1

【答案】B=75°， C=60°， AC=或C=120°， B=15°，AC=

【解析】试题分析：方法一：先由正弦定理求得或，再用三角形内角和定理求得，最后用正弦定理求。

方法二：先由余弦定理求得，再用正弦定理求得或，最后用三角形内角和定理求。

试题解析：方法一：

在△ABC中，A=45°，，BC=2，

由正弦定理得,

∴,

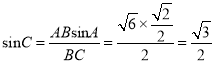又，所以。

∴或。

①当时， ,

由正弦定理得,

∴。

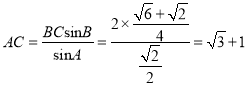②当时，

由正弦定理得,

∴。

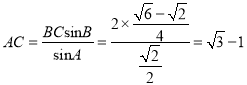综上或。

方法二：

由余弦定理：BC2=AC2+AB2﹣2ABACcos∠A

∴，

整理得 ，

解得：AC=或AC=．

∴，BC=2，AC=或AC=，，BC=2，

在△ABC中由正弦定理得，

可得：sinC=，

∵A=45°，A+B+C=180°

∴0＜C＜135°

当C=60°时，则B=180°﹣45°﹣60°=75°．

当C=120°时，则B=180°﹣45°﹣120°=15°．

综上或。