题目内容
已知函数 对任意
对任意 都满足
都满足 ,且
,且 ,数列
,数列 满足:
满足: ,
, .
.
(Ⅰ)求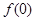 及
及 的值;
的值;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)若 ,试问数列
,试问数列 是否存在最大项和最小项?若存在,求出最大项和最小项;若不存在,请说明理由.
是否存在最大项和最小项?若存在,求出最大项和最小项;若不存在,请说明理由.
(Ⅰ) ,
, ,(Ⅱ)
,(Ⅱ) ,(Ⅲ)当
,(Ⅲ)当 ,即
,即 时,
时, 的最大项为
的最大项为 .当
.当 ,即
,即 时,
时, 的最小项为
的最小项为 .
.
解析试题分析:(Ⅰ)对应抽象函数,一般方法为赋值法. 在 中,取
中,取 ,得
,得 ,在
,在 中,取
中,取 ,得
,得 ,(Ⅱ)在
,(Ⅱ)在 中,令
中,令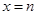 ,
, ,得
,得 ,即
,即 .所以
.所以 是等差数列,公差为2,又首项
是等差数列,公差为2,又首项 ,所以
,所以 ,
, .(Ⅲ)研究数列
.(Ⅲ)研究数列 是否存在最大项和最小项,关键看通项公式的特征.令
是否存在最大项和最小项,关键看通项公式的特征.令 ,则
,则 ,显然
,显然 ,又因为
,又因为 ,所以当
,所以当 ,即
,即 时,
时, 的最大项为
的最大项为 .当
.当 ,即
,即 时,
时, 的最小项为
的最小项为
解:(Ⅰ)在 中,取
中,取 ,得
,得 ,
,
在 中,取
中,取 ,得
,得 , 2分
, 2分
(Ⅱ)在 中,令
中,令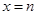 ,
, ,
,
得 ,即
,即 .
.
所以 是等差数列,公差为2,又首项
是等差数列,公差为2,又首项 ,所以
,所以 ,
, . 6分
. 6分
(Ⅲ)数列 存在最大项和最小项
存在最大项和最小项
令 ,则
,则 ,
,
显然 ,又因为
,又因为 ,
,
所以当 ,即
,即 时,
时, 的最大项为
的最大项为 .
.
当 ,即
,即 时,
时, 的最小项为
的最小项为 . 13分
. 13分
考点:等差数列,赋值法研究抽象函数

练习册系列答案
相关题目
 有最大值,
有最大值, 的单调区间.
的单调区间.
 ,其中
,其中 ,
, 为正整数,
为正整数, ,
, ,
, 均为常数,曲线
均为常数,曲线 在
在 处的切线方程为
处的切线方程为 .
. 的最大值;
的最大值; 都有
都有 .(
.( 为自然对数的底)
为自然对数的底) (a是常数,a∈R)
(a是常数,a∈R) 的解集.
的解集. 恰有两个不同的零点,求a的取值范围.
恰有两个不同的零点,求a的取值范围. ,其
,其 中为常数,
中为常数, .
. 时,求曲线
时,求曲线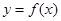 在点
在点 处的切线方程;
处的切线方程; 的极大值为
的极大值为 ?若存在,求出
?若存在,求出 ,用
,用 表示
表示 当
当 时的函数值中整数值的个数.
时的函数值中整数值的个数. ,求
,求 .
. ,若
,若 ,求
,求 的最小值.
的最小值.
 .
. 时,判断
时,判断 在
在 的单调性,并用定义证明.
的单调性,并用定义证明. ,不等式
,不等式  恒成立,求
恒成立,求 的取值范围;
的取值范围;