题目内容
(本题满分12分)设A>0,A≠1,函数 有最大值,
有最大值,
求函数 的单调区间.
的单调区间.
单调减区间为(-3,-1],单调增区间为[-1,1).
解析试题分析:函数 有最大值,
有最大值, 有最小值,由对数函数的性质可知
有最小值,由对数函数的性质可知 ,由
,由 型复合函数的单调性知,在
型复合函数的单调性知,在 的定义域内,
的定义域内, 的增区间为原函数的减区间,
的增区间为原函数的减区间, 的减区间为原函数的增区间.
的减区间为原函数的增区间.
解:设 .
.
当x=1时,t有最小值lg2, 2分
又因为函数 有最大值,所以
有最大值,所以 . 4分
. 4分
又因为 的定义域为{x|-3<x<1}, 6分
的定义域为{x|-3<x<1}, 6分
令 ,x∈(-3,1),则
,x∈(-3,1),则 .
.
因为 在定义域内是减函数,
在定义域内是减函数,
当x∈(-3,-1]时,u=-(x+1)2+4是增函数,所以f(x)在(-3,-1]上是减函数.
同理,f(x)在[-1,1)上是增函数. 10分
故f(x)的单调减区间为(-3,-1],单调增区间为[-1,1). 12分
考点:对数函数,指数函数的性质,复合函数的单调性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 在定义域内恒成立;
在定义域内恒成立; 时,
时, 恒成立,求m的取值范围.
恒成立,求m的取值范围.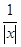 .
. (
( 为定义域)图像上的点到坐标原点的距离为函数的
为定义域)图像上的点到坐标原点的距离为函数的 与
与 是否存在长距与短距,若存在,请求出;
是否存在长距与短距,若存在,请求出; 的短距小于1;
的短距小于1; 是否存在实数
是否存在实数 ,使得函数
,使得函数 的短距不小于2,若存在,请求出
的短距不小于2,若存在,请求出
 的最小值;
的最小值;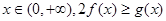 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. (a是常数,a∈R)
(a是常数,a∈R) 的解集.
的解集. 恰有两个不同的零点,求a的取值范围.
恰有两个不同的零点,求a的取值范围. ,x∈
,x∈ ,
, .
. 时,求函数f(x)的最小值;
时,求函数f(x)的最小值; 的最小值为4,求实数
的最小值为4,求实数
 对任意
对任意 都满足
都满足 ,且
,且 ,数列
,数列 满足:
满足: ,
, .
.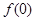 及
及 的值;
的值; 的通项公式;
的通项公式; ,试问数列
,试问数列 是否存在最大项和最小项?若存在,求出最大项和最小项;若不存在,请说明理由.
是否存在最大项和最小项?若存在,求出最大项和最小项;若不存在,请说明理由.
 .
. 时,判断
时,判断 在
在 的单调性,并用定义证明;
的单调性,并用定义证明; ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围;
的取值范围;