题目内容
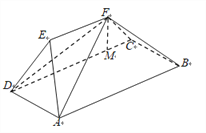
【题目】如图,在五面体![]() 中,底面
中,底面![]() 为正方形,
为正方形, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() .
.

(1)求证: ![]() ;
;
(2)若![]() ,
, ![]() ,求五面体
,求五面体![]() 的体积.
的体积.
【答案】(1)见解析(2) ![]()
【解析】试题分析:
(1)要证线线垂直,可先证线面垂直,已知有![]() ,因此只要再证
,因此只要再证![]() ,这可由面面垂直的性质定理得
,这可由面面垂直的性质定理得![]() 平面
平面![]() ,从而得到结论;
,从而得到结论;
(2)这个多面体可分拆为一个三棱锥![]() 和一个四棱锥
和一个四棱锥![]() ,它们的高易作出,分别求出体积即可.
,它们的高易作出,分别求出体积即可.
试题解析:
(Ⅰ)因为平面ABCD⊥平面CDEF,
平面ABCD∩平面CDEF=CD,AD⊥CD,
所以AD⊥平面CDEF,又CF平面CDEF,
则AD⊥CF.
又因为AE⊥CF,AD∩AE=A,
所以CF⊥平面AED,DE平面AED,
从而有CF⊥DE.
(Ⅱ)连接FA,FD,过F作FM⊥CD于M,
因为平面ABCD⊥平面CDEF且交线为CD,FM⊥CD,
所以FM⊥平面ABCD.
因为CF=DE,DC=2EF=4,且CF⊥DE,
所以FM=CM=1,
所以五面体的体积V=VF-ABCD+VA-DEF=![]() +
+![]() =
=![]() .
.

练习册系列答案
相关题目