题目内容
15.已知集合A={x|$\frac{π}{4}$≤x≤$\frac{π}{2}$},函数f(x)=4sin2($\frac{π}{4}$+x)-2$\sqrt{3}$cos2x-1,x∈A,求f(x)的最大值及最小值.分析 由三角函数公式化简可得f(x)=4sin(2x-$\frac{π}{3}$)+1,由$\frac{π}{4}$≤x≤$\frac{π}{2}$结合不等式的性质和三角函数可得最值.
解答 解:由三角函数公式化简可得f(x)=4sin2($\frac{π}{4}$+x)-2$\sqrt{3}$cos2x-1
=4×$\frac{1-cos(\frac{π}{2}+2x)}{2}$-2$\sqrt{3}$cos2x-1=2sin2x-2$\sqrt{3}$cos2x+1
=4($\frac{1}{2}$sin2x-$\frac{\sqrt{3}}{2}$cos2x)+1=4sin(2x-$\frac{π}{3}$)+1
∵$\frac{π}{4}$≤x≤$\frac{π}{2}$,∴$\frac{π}{6}$≤2x-$\frac{π}{3}$≤$\frac{5π}{6}$,
∴$\frac{1}{2}$≤sin(2x-$\frac{π}{3}$)≤1,
∴3≤4sin(2x-$\frac{π}{3}$)+1≤5,
∴f(x)的最大值为5,最小值为3
点评 本题考查三角函数的最值,涉及和差角的三角函数,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
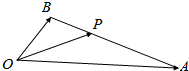 如图,在△ABC中,已知P为线段AB上一点,且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$.
如图,在△ABC中,已知P为线段AB上一点,且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$.