��Ŀ����
����Ŀ��ij��ҵ����һ�ֲ�Ʒ�����ݾ��飬���Ʒ��![]() ���ղ���
���ղ���![]() �������֮�������ϵ,
�������֮�������ϵ, ������
������![]() ��������
Ϊ��������![]() ����֪ÿ����1����ϸ�IJ�Ʒ��ӯ��2��Ԫ����ÿ����1�����Ʒ������1��Ԫ��ע:��Ʒ��=��Ʒ��/�������� ��
����֪ÿ����1����ϸ�IJ�Ʒ��ӯ��2��Ԫ����ÿ����1�����Ʒ������1��Ԫ��ע:��Ʒ��=��Ʒ��/�������� ��![]() ��ʾÿ����10����Ʒ����1����Ʒ������Ϊ�ϸ�Ʒ��.
��ʾÿ����10����Ʒ����1����Ʒ������Ϊ�ϸ�Ʒ��.
��1���Խ��������ֲ�Ʒÿ���ӯ����![]() ����Ԫ����ʾΪ�ղ���
����Ԫ����ʾΪ�ղ���![]() ��������ĺ�����
������������
��2�����ղ���Ϊ����ʱ���ɻ���������?
���𰸡���1��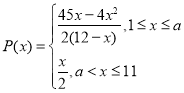 ����2��������.
����2��������.
��������
��1������ÿ���Ӯ��ΪP��x�����ղ�����x������Ʒ�ʣ�1��Q����2���ղ�����x������Ʒ�ʣ�Q����1���������ɵõ�P��x����x�ĺ���ʽ��
��2����a��x��11ʱ�����P��x�������ֵ����1��x��aʱ����12��x��t�����û�������ʽ�ɵ�x��9ʱ���Ⱥų������ʿɷ������۵ã���1��a��3ʱ����x��11ʱ��ȡ��������� 3��a��9ʱ�����ø��Ϻ����ĵ����Կɵõ�x��aʱȡ���������9��a��11ʱ�����ղ���Ϊ9���ʱ��ȡ���������
��1����![]() ʱ��
ʱ��![]() ��
��
��![]() .
.
��![]() ʱ��
ʱ��![]() ��
��
��![]() .
.
���ϣ���ӯ����![]() ����Ԫ�����ղ���x��������ĺ�����ϵʽΪ
����Ԫ�����ղ���x��������ĺ�����ϵʽΪ
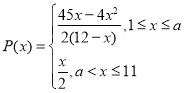 ��������a��������
��������a��������![]() ��.
��.
��2����![]() ʱ��
ʱ��![]() �������ֵΪ55��Ԫ.
�������ֵΪ55��Ԫ.
��![]() ʱ��
ʱ��![]() ����
����![]() ����
����![]() ��
��
��ʱ��![]() ��
��
��Ȼ�����ҽ���![]() ����
����![]() ʱ��
ʱ��![]() �����ֵ��Ϊ13.5��Ԫ.
�����ֵ��Ϊ13.5��Ԫ.
��![]() ����
����![]() ��
��
���![]() ����ȥ����
����ȥ����![]() ��
��
��i����![]() ʱ���ղ���Ϊ11���ʱ���ɻ���������5.5��Ԫ.
ʱ���ղ���Ϊ11���ʱ���ɻ���������5.5��Ԫ.
��ii����![]() ʱ��
ʱ��![]() ʱ��
ʱ��
����![]() �ɿ������ɺ���
�ɿ������ɺ���![]() ��
��![]() ���϶��ɵ�.
���϶��ɵ�.
��Ϊ![]() ������
������![]() ����
����![]() ��
��![]() ��������
��������
��![]() ��
��![]() ��������������
��������������![]() ��
��![]() ��������
��������
�ʵ��ղ���Ϊa���ʱ���ɻ���������![]() ��Ԫ.
��Ԫ.
��iii����![]() ʱ���ղ���Ϊ9���ʱ���ɻ���������13.5��Ԫ.
ʱ���ղ���Ϊ9���ʱ���ɻ���������13.5��Ԫ.

����Ŀ��Ϊ����ѧ��������˽�����ѧʷ��֪ʶ��ij��ѧ�߶��꼶�ٰ���һ����Ѱ���ܵ��㼣��������ѧ������������ѧʷ֪ʶ�����������800��ѧ���μ�����ξ�����Ϊ�˽Ȿ�ξ����ijɼ���������г�ȡ�˲���ѧ���ijɼ����÷־�Ϊ����������Ϊ100�֣�����ͳ�ƣ�ͳ�ƽ�����±�.�������Ƶ�ʷֲ�������������⣺
��� | ���飨������ | ����ֵ | Ƶ���������� | Ƶ�� |
1 |
| 65 | �� | 0.12 |
2 |
| 75 | 20 | �� |
3 |
| 85 | �� | 0.24 |
4 |
| 95 | �� | �� |
�ϼ� | 50 | 1 |
��1�����Ƶ�ʷֲ����еĿո�
��2���涨�ɼ�������85�ֵ�ͬѧ�ܻ�������ڲμӵ�800��ѧ���д���ж�����ͬѧ��
��3��������ͳ�����ݵķ�������һ�������㷨����ͼ���������![]() ��ֵ.
��ֵ.

