题目内容
函数 .
.
(1)讨论 的单调性;
的单调性;
(2)设 ,证明:
,证明: .
.
(1)(1)当 时,
时, 在
在 上是增函数,在
上是增函数,在 上是减函数,在
上是减函数,在 上是增函数;(2)当
上是增函数;(2)当 时,
时, 在
在 上是增函数;(iii)当
上是增函数;(iii)当 时,
时, 在是
在是 上是增函数,在
上是增函数,在 上是减函数,在
上是减函数,在 上是增函数;(2)详见试题分析.
上是增函数;(2)详见试题分析.
解析试题分析:(1)首先求函数 的定义域,
的定义域, 的导数:
的导数: ,再分
,再分 ,
, ,
, 三种情况,讨论函数
三种情况,讨论函数 的单调性;(2)先在(1)的基础上,当
的单调性;(2)先在(1)的基础上,当 时,由
时,由 的单调性得
的单调性得 .同理当
.同理当 时,由
时,由 的单调性得
的单调性得 .下面再用数学归纳法证明
.下面再用数学归纳法证明 .
.
(1) 的定义域为
的定义域为 .
.
(1)当 时,若
时,若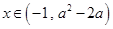 ,则
,则 在
在 上是增函数;若
上是增函数;若 则
则 在
在 上是减函数;若
上是减函数;若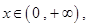 则
则 在
在 上是增函数.
上是增函数.
(2)当 时,
时, 成立当且仅当
成立当且仅当 在
在 上是增函数.
上是增函数.
(iii)当 时,若
时,若 ,则
,则 在是
在是 上是增函数;若
上是增函数;若 ,则
,则 在
在 上是减函数;若
上是减函数;若 ,则
,则 在
在 上是增函数.
上是增函数.
(2)由(1)知,当 时,
时, 在
在 是增函数.当
是增函数.当 时,
时, ,即
,即 .又由(1)知,当
.又由(1)知,当 时,
时, 在
在 上是减函数;当
上是减函数;当 时,
时, ,即
,即 .下面用数学归纳法证明
.下面用数学归纳法证明 .
.
(1)当 时,由已知
时,由已知 ,故结论成立;
,故结论成立;
(2)假设当 时结论成立,即
时结论成立,即 .当
.当 时,
时, ,即当
,即当 时有
时有 ,结论成立.根据(1)、(2)知对任何
,结论成立.根据(1)、(2)知对任何 结论都成立.
结论都成立.
考点:1.利用导数研究函数的单调性;2.利用数学归纳法证明数列不等式.

练习册系列答案
相关题目
 在
在 与
与 处都取得极值.
处都取得极值.  ,
, 的值;
的值; ,若对任意的
,若对任意的 ,总存在
,总存在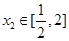 ,使得:
,使得: ,求实数
,求实数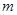 的取值范围.
的取值范围. ,
, .
.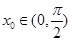 ,使
,使 ;
; ,使
,使 ,且对(1)中的
,且对(1)中的 .
. ;
; .
. .
. .
. ,求函数f(x)和f′(x)的公共递减区间的长度;
,求函数f(x)和f′(x)的公共递减区间的长度; .
. 在区间
在区间 上的最大值;
上的最大值; 存在3条直线与曲线
存在3条直线与曲线 相切,求t的取值范围;
相切,求t的取值范围; 分别存在几条直线与曲线
分别存在几条直线与曲线