题目内容
向量a,b,c满足:|a|=1,|b|=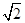 ,b在a方向上的投影为
,b在a方向上的投影为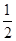 ,(a-c)·(b-c)=0,则|c|的最大值是________.
,(a-c)·(b-c)=0,则|c|的最大值是________.
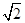 ,b在a方向上的投影为
,b在a方向上的投影为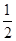 ,(a-c)·(b-c)=0,则|c|的最大值是________.
,(a-c)·(b-c)=0,则|c|的最大值是________.1+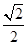
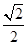
由投影公式可得 =b·a=
=b·a=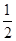 ,∴|b+a|2=|a|2+|b|2+2a·b=4⇒|b+a|=2.由(a-c)·(b-c)=a·b-c·(a+b)+c2=0,整理得
,∴|b+a|2=|a|2+|b|2+2a·b=4⇒|b+a|=2.由(a-c)·(b-c)=a·b-c·(a+b)+c2=0,整理得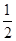 +|c|2=|c|·|a+b|cos θ≤2|c|,解不等式
+|c|2=|c|·|a+b|cos θ≤2|c|,解不等式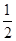 +|c|2-2|c|≤0,得|c|≤1+
+|c|2-2|c|≤0,得|c|≤1+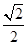 ,即|c|的最大值为1+
,即|c|的最大值为1+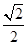
 =b·a=
=b·a=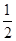 ,∴|b+a|2=|a|2+|b|2+2a·b=4⇒|b+a|=2.由(a-c)·(b-c)=a·b-c·(a+b)+c2=0,整理得
,∴|b+a|2=|a|2+|b|2+2a·b=4⇒|b+a|=2.由(a-c)·(b-c)=a·b-c·(a+b)+c2=0,整理得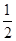 +|c|2=|c|·|a+b|cos θ≤2|c|,解不等式
+|c|2=|c|·|a+b|cos θ≤2|c|,解不等式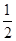 +|c|2-2|c|≤0,得|c|≤1+
+|c|2-2|c|≤0,得|c|≤1+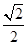 ,即|c|的最大值为1+
,即|c|的最大值为1+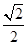

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 、
、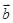 、
、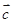 中任意二个都不共线,但
中任意二个都不共线,但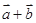 与
与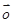
 b,m∈R,k、t为正实数.
b,m∈R,k、t为正实数.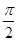
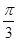
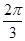
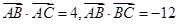 则
则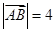 ;
;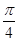
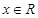 ,都有sinx≤1,则
,都有sinx≤1,则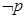 为:存在
为:存在 ,则α与β的夹角θ的取值范围是 .
,则α与β的夹角θ的取值范围是 . ;③若△ABC中,a="5,b=8," c=7,则
;③若△ABC中,a="5,b=8," c=7,则 ·
· =20;④若非零向量a,b满足|a+b|=|b|,则|2b|>|a+2b|.其中所有真命题的序号是 .
=20;④若非零向量a,b满足|a+b|=|b|,则|2b|>|a+2b|.其中所有真命题的序号是 .
 =
=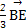
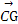 =2
=2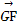
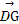 =
=
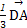 +
+ =
=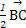
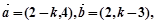 若
若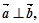 则
则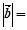 .
.