题目内容
已知向量a＝(1，2)，b＝(－2，m)，x＝a＋(t2＋1)b，y＝－ka＋
b，m∈R，k、t为正实数．
(1)若a∥b，求m的值；
(2)若a⊥b，求m的值；
(3)当m＝1时，若x⊥y，求k的最小值．
b，m∈R，k、t为正实数．(1)若a∥b，求m的值；
(2)若a⊥b，求m的值；
(3)当m＝1时，若x⊥y，求k的最小值．
（1）m＝－4.（2）m＝1（3）2.
(1)因为a∥b，所以1·m－2·(－2)＝0，解得m＝－4.
(2)因为a⊥b，所以a·b＝0，
所以1·(－2)＋2m＝0，解得m＝1.
(3)当m＝1时，a·b＝0.
因为x⊥y，所以x·y＝0.
则x·y＝－ka2＋
a·b＋(t＋)b2＝0.
因为t＞0，所以k＝t＋≥2，当t＝1时取等号，
即k的最小值为2.
(2)因为a⊥b，所以a·b＝0，
所以1·(－2)＋2m＝0，解得m＝1.
(3)当m＝1时，a·b＝0.
因为x⊥y，所以x·y＝0.
则x·y＝－ka2＋
a·b＋(t＋)b2＝0.因为t＞0，所以k＝t＋
≥2，当t＝1时取等号，即k的最小值为2.
练习册系列答案
相关题目
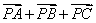＝0，设
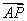＝λ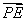
，则λ的值为( )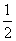
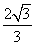
两两所成的角相等，且
，则
等于（）
或
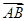在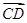
方向上的投影为( )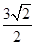
(
)是
所在的平面内的点，且
.
；②
的最小值一定是
；
、
个.
个.
个.
个.
＋
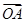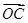＝－2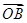
，则△AOB与△AOC的面积之比为________．
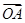＋x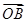
＋
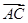＝0的解集为( )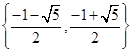
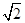，b在a方向上的投影为
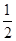，(a－c)·(b－c)＝0，则|c|的最大值是________．
.
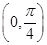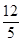，求sin 
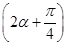的值．