题目内容
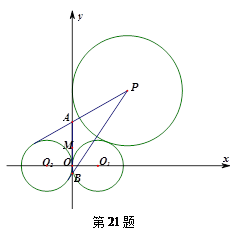
如图,在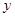 轴右侧的动圆⊙
轴右侧的动圆⊙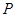 与⊙
与⊙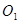 :
: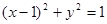 外切,并与
外切,并与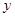 轴相切.
轴相切.
(Ⅰ)求动圆的圆心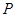 的轨迹
的轨迹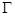 的方程;
的方程;
(Ⅱ)过点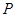 作⊙
作⊙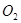 :
: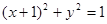 的两条切线,分别交
的两条切线,分别交 轴于
轴于 两点,设
两点,设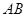 中点为
中点为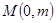 .求
.求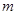 的取值范围.
的取值范围.
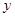 轴右侧的动圆⊙
轴右侧的动圆⊙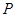 与⊙
与⊙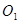 :
: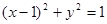 外切,并与
外切,并与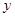 轴相切.
轴相切.(Ⅰ)求动圆的圆心
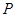 的轨迹
的轨迹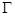 的方程;
的方程;(Ⅱ)过点
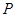 作⊙
作⊙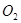 :
: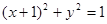 的两条切线,分别交
的两条切线,分别交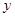 轴于
轴于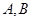 两点,设
两点,设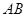 中点为
中点为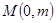 .求
.求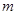 的取值范围.
的取值范围.
(Ⅰ)由题意,点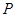 到点
到点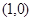 的距离等于它到直线
的距离等于它到直线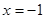 的距离,故
的距离,故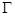 是抛物线,方程为
是抛物线,方程为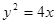 (
(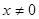 ).…………………………………
).………………………………… 分
分
注:由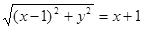 化简同样给分;不写
化简同样给分;不写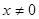 不扣分.
不扣分.
(Ⅱ)设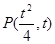 (
(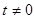 ),切线斜率为
),切线斜率为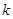 , 则切线方程为
, 则切线方程为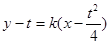 ,即
,即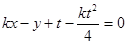 .…………………………
.………………………… 分
分
由题意,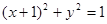 的圆心
的圆心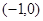 到切线的距离
到切线的距离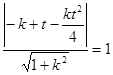 ,…………………………
,………………………… 分
分
两边平方并整理得: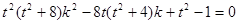 .……………………
.…………………… 分
分
该方程的两根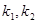
 就是两条切线的斜率,由韦达定理:
就是两条切线的斜率,由韦达定理: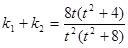 . ①
. ①
另一方面,在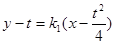 ,
,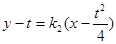 中
中 令
令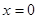 可得
可得 两点的纵坐标
两点的纵坐标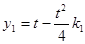 ,
,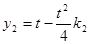 ,故
,故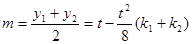 , ②
, ②
将①代入②,得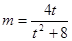
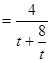 ,……………………………
,……………………………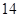 分
分
故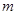 的取值范围是
的取值范围是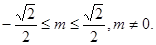
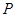 到点
到点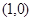 的距离等于它到直线
的距离等于它到直线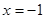 的距离,故
的距离,故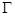 是抛物线,方程为
是抛物线,方程为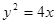 (
(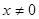 ).…………………………………
).…………………………………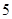 分
分注:由
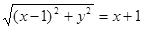 化简同样给分;不写
化简同样给分;不写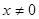 不扣分.
不扣分.(Ⅱ)设
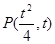 (
(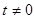 ),切线斜率为
),切线斜率为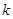 , 则切线方程为
, 则切线方程为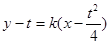 ,即
,即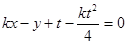 .…………………………
.…………………………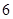 分
分由题意,
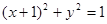 的圆心
的圆心 到切线的距离
到切线的距离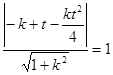 ,…………………………
,…………………………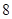 分
分两边平方并整理得:
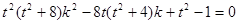 .……………………
.……………………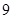 分
分该方程的两根
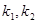
 就是两条切线的斜率,由韦达定理:
就是两条切线的斜率,由韦达定理: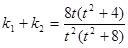 . ①
. ①另一方面,在
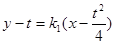 ,
,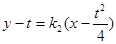 中
中 令
令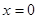 可得
可得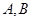 两点的纵坐标
两点的纵坐标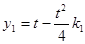 ,
,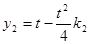 ,故
,故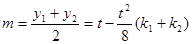 , ②
, ②将①代入②,得
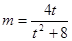
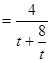 ,……………………………
,……………………………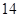 分
分故
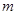 的取值范围是
的取值范围是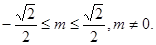
略

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
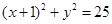 的圆心为C,A(1,0)是圆内一定点,Q为圆周上任意一点,线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程是( )
的圆心为C,A(1,0)是圆内一定点,Q为圆周上任意一点,线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程是( )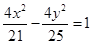
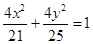
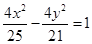
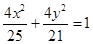
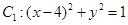 ,圆
,圆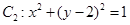 ,圆
,圆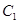 ,
,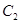 关于直线
关于直线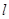 对称.
对称.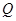 ,使
,使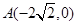 点的距离减去
点的距离减去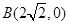 点的距离的差为
点的距离的差为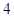 ,如果存在求出
,如果存在求出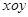 中,已知“葫芦”曲线
中,已知“葫芦”曲线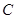 由圆弧
由圆弧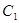 与圆弧
与圆弧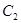 相接而成,两相接点
相接而成,两相接点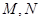 均在直线
均在直线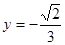 上.圆弧
上.圆弧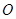 ,半径为
,半径为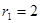 ;圆弧
;圆弧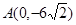 .
.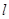 :
: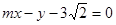 与“葫芦”曲线
与“葫芦”曲线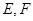 两点.当
两点.当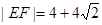 时,求直线
时,求直线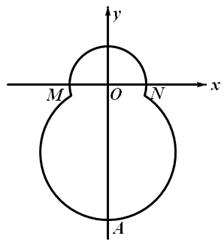
 以
以 为圆心且经过原点O.
为圆心且经过原点O. ,写出圆
,写出圆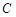 的方程;
的方程;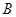 的坐标为
的坐标为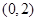 ,设
,设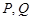 分别是直线
分别是直线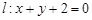 和圆
和圆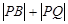 的最小值及此时点
的最小值及此时点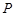 的坐标.
的坐标.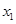 、
、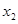 是关于x的方程
是关于x的方程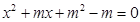 的两个不相等的实数根,那么过两点
的两个不相等的实数根,那么过两点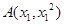 ,
,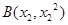 的直线与圆
的直线与圆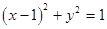 的位置关系是( )
的位置关系是( )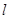 与圆
与圆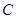 相交于点
相交于点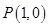 和点
和点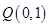 。
。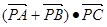 的值是 。
的值是 。