题目内容
(本小题满分8分)已知圆c:(x-1)2+y2=4,直线l:mx-y-1=0
(1)当m=–1时,求直线l圆c所截的弦长;
(2)求证:直线l与圆c有两个交点。
(1)当m=–1时,求直线l圆c所截的弦长;
(2)求证:直线l与圆c有两个交点。
解:(1)当m=–1时,直线l:x+y+1=0,圆心c(1,0),半径r=2,则圆心c到直线l:x+y+1=0的距离为
d=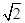
所以直线l被圆c所截的弦长为

消去y得(1+m2)x2-2(m+1)x-2=0……………………6分
因为D=4(1+m)2+8(1+m2)>0
所以直线l与圆c有两个交点。……………………8分
d=
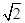
所以直线l被圆c所截的弦长为

消去y得(1+m2)x2-2(m+1)x-2=0……………………6分
因为D=4(1+m)2+8(1+m2)>0
所以直线l与圆c有两个交点。……………………8分
略

练习册系列答案
相关题目
 的圆
的圆 与圆
与圆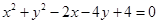 相交,它们的公共弦平行于直线
相交,它们的公共弦平行于直线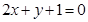 .
.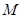 经过一定点
经过一定点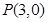 ,且与圆
,且与圆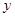 轴右侧的动圆⊙
轴右侧的动圆⊙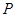 与⊙
与⊙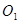 :
: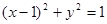 外切,并与
外切,并与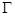 的方程;
的方程;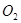 :
: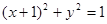 的两条切线,分别交
的两条切线,分别交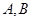 两点,设
两点,设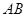 中点为
中点为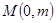 .求
.求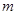 的取值范围.
的取值范围.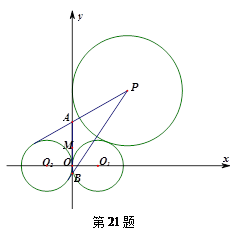
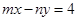 与⊙O: x2+y2= 4没有交点,则过点
与⊙O: x2+y2= 4没有交点,则过点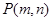 的直线与椭圆
的直线与椭圆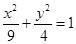 的交点个数是( )
的交点个数是( ) 中,
中,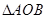 和
和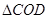 为等腰直角三角形,
为等腰直角三角形,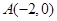 ,
,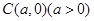 设
设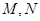 .
.
 相切,求直线
相切,求直线 截圆N所得弦长为4,求圆N的标准方程;
截圆N所得弦长为4,求圆N的标准方程;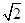 ,若存在,求此时圆N的标准方程;若不存在,说明理由.
,若存在,求此时圆N的标准方程;若不存在,说明理由.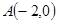 ,动点
,动点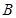 是圆
是圆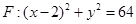 (
(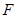 为圆心)上一点,线段
为圆心)上一点,线段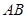 的垂直平分线交
的垂直平分线交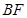 于点
于点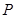 .
. 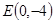 的直线
的直线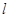 交
交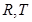 ,且满足
,且满足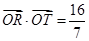 (
( 为原点).若存在,求直线
为原点).若存在,求直线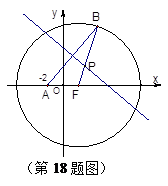
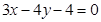 被圆
被圆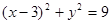 截得的弦长是( )
截得的弦长是( )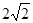
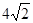
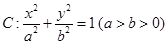 的离心率为
的离心率为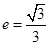 ,以原点为圆心,椭圆短半轴长为半径的圆与直线
,以原点为圆心,椭圆短半轴长为半径的圆与直线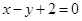 相切,
相切,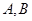 分别是椭圆的左右两个顶点,
分别是椭圆的左右两个顶点, 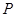 为椭圆
为椭圆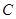 上的动点.
上的动点.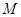 为过
为过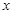 轴的直线上的点,若
轴的直线上的点,若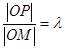 ,求点
,求点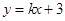 与圆
与圆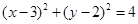 相交于
相交于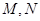 两点,若
两点,若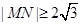 ,则
,则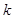 的取值范围是 .
的取值范围是 .