题目内容
随机抽取某厂的某种产品200件,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而生产1件次品亏损2万元,设一件产品获得的利润为X(单位:万元).
(1)求X的分布列;
(2)求1件产品的平均利润(即X的数学期望);
(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品率提高为70%.如果此时要求生产1件产品获得的平均利润不小于4.73万元,则三等品率最多是多少?
(1)求X的分布列;
(2)求1件产品的平均利润(即X的数学期望);
(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品率提高为70%.如果此时要求生产1件产品获得的平均利润不小于4.73万元,则三等品率最多是多少?
(1)X的分布列:
(2)  万元
万元
(3)三等品率最多是6件.
| X | -2 | 1 | 2 | 6 |
| P | 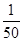 |  |  | 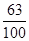 |
 万元
万元(3)三等品率最多是6件.
(1)先确定X可能取的值有-2,1,2,6.然后求出每一个值对应的概率,列出分布列即可.
(2)根据期望等于每一个X值与其对应的概率积之和求解即可.
(3)可先设三等品有x件,则 ,然后参照(1)(2)的作法求出分布列及期望值,再根据E(X)
,然后参照(1)(2)的作法求出分布列及期望值,再根据E(X) ,建立关于x的不等式,求出x的最大值
,建立关于x的不等式,求出x的最大值
(1)X的分布列:
(2)  万元……………10分
万元……………10分
(3)设三等品有 件,则
件,则
X的分布列:

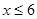
所以三等品率最多是6件.
(2)根据期望等于每一个X值与其对应的概率积之和求解即可.
(3)可先设三等品有x件,则
 ,然后参照(1)(2)的作法求出分布列及期望值,再根据E(X)
,然后参照(1)(2)的作法求出分布列及期望值,再根据E(X) ,建立关于x的不等式,求出x的最大值
,建立关于x的不等式,求出x的最大值(1)X的分布列:
| X | -2 | 1 | 2 | 6 |
| P | 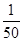 |  |  | 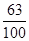 |
 万元……………10分
万元……………10分(3)设三等品有
 件,则
件,则
X的分布列:
| X | -2 | 1 | 2 | 6 |
| P |  |  |  |  |

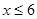
所以三等品率最多是6件.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 是一个离散型随机变量,其分布列如下表,试求随机变量
是一个离散型随机变量,其分布列如下表,试求随机变量 与方差
与方差 .
.
 ,求
,求 ,其他三项挑战失败的概率分别为
,其他三项挑战失败的概率分别为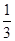 .
.



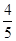
 ,求
,求
 ,规定使用“七局四胜制”,即先赢四局者胜.
,规定使用“七局四胜制”,即先赢四局者胜. ,三人都做对的概率是
,三人都做对的概率是 ,三人全做错的概率是
,三人全做错的概率是 ,已知乙做对这道题的概率大于丙做对这道题的概率.设三人中做对这道题的人数为
,已知乙做对这道题的概率大于丙做对这道题的概率.设三人中做对这道题的人数为 ,则随机变量
,则随机变量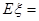 .
. ,求随机变量
,求随机变量 以及方差
以及方差
 个白球,这些红球和白球除了颜色不同之外,其余都相同,从袋中同时取两个球.
个白球,这些红球和白球除了颜色不同之外,其余都相同,从袋中同时取两个球.