题目内容
如果甲乙两个乒乓球选手进行比赛,而且他们在每一局中获胜的概率都是 ,规定使用“七局四胜制”,即先赢四局者胜.
,规定使用“七局四胜制”,即先赢四局者胜.
(1)试分别求甲打完4局、5局才获胜的概率;
(2)设比赛局数为ξ,求ξ的分布列及期望.
 ,规定使用“七局四胜制”,即先赢四局者胜.
,规定使用“七局四胜制”,即先赢四局者胜.(1)试分别求甲打完4局、5局才获胜的概率;
(2)设比赛局数为ξ,求ξ的分布列及期望.
(1)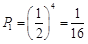 ;
;  ;
;
(2)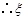 的分布列为
的分布列为
 =
=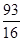
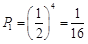 ;
;  ;
;(2)
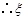 的分布列为
的分布列为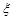 | 4 | 5 | 6 | 7 |
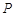 | 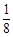 | 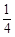 | 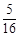 | 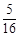 |
 =
=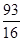
(1) (i)甲打完4局才获胜说明4局甲全胜.所以其概率为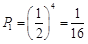
(ii)甲打完5局才获胜,即甲在前4局比赛中胜3局且第5局胜.所以甲打完5局才获胜的概率为
(2)先确定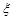 的可能取值为4,5,6,7,然后再求出
的可能取值为4,5,6,7,然后再求出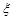 取每个值对应的概率,再列出分布列,根据期望公式求出期望值即可
取每个值对应的概率,再列出分布列,根据期望公式求出期望值即可
(1)①甲打完4局才获胜的概率为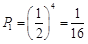 ;
;
②甲打完5局才获胜,即甲在前4局比赛中胜3局且第5局胜,则甲打完5局才获胜的概率为 ;
;
(2) 的可能取值为4,5,6,7.
的可能取值为4,5,6,7.
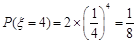 ;
;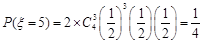 ;
;
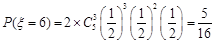 ;
;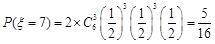 .
.
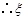 的分布列为
的分布列为
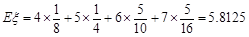 =
=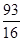
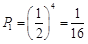
(ii)甲打完5局才获胜,即甲在前4局比赛中胜3局且第5局胜.所以甲打完5局才获胜的概率为

(2)先确定
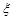 的可能取值为4,5,6,7,然后再求出
的可能取值为4,5,6,7,然后再求出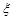 取每个值对应的概率,再列出分布列,根据期望公式求出期望值即可
取每个值对应的概率,再列出分布列,根据期望公式求出期望值即可(1)①甲打完4局才获胜的概率为
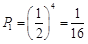 ;
;②甲打完5局才获胜,即甲在前4局比赛中胜3局且第5局胜,则甲打完5局才获胜的概率为
 ;
;(2)
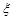 的可能取值为4,5,6,7.
的可能取值为4,5,6,7.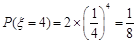 ;
;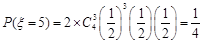 ;
;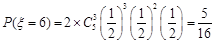 ;
;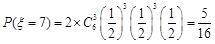 .
.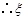 的分布列为
的分布列为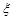 | 4 | 5 | 6 | 7 |
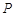 | 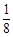 | 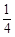 | 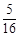 | 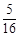 |
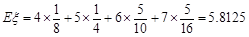 =
=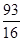

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
 =____________.
=____________. 内,不等式
内,不等式 确定的平面区域为
确定的平面区域为 ,不等式组
,不等式组 确定的平面区域为
确定的平面区域为 .
. 的概率;
的概率; 个点,连续取
个点,连续取 次,得到
次,得到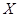 ,求
,求 的分布列和数学期望.
的分布列和数学期望. 表示取出的球的最大号码,则
表示取出的球的最大号码,则 ( )
( ) 





 分,负者得
分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多 分或打满
分或打满 局时停止.设甲在每局中获胜的概率为
局时停止.设甲在每局中获胜的概率为 ,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为 .
. 的值;
的值; 表示比赛停止时比赛的局数,求随机变量
表示比赛停止时比赛的局数,求随机变量 .
. 点数大于
点数大于 4时,质点向前跳两步.
4时,质点向前跳两步. 质点到达的正整数记为
质点到达的正整数记为 ,求E
,求E