题目内容
(14分)袋中有大小相同的小球6个,其中红球2个,黄球4个,规定1个红球得2分,1个黄球得1分,从袋中任取3个球,记所取3个球的分数之和为 ,求随机变量
,求随机变量 的分布列和期望
的分布列和期望 以及方差
以及方差
 ,求随机变量
,求随机变量 的分布列和期望
的分布列和期望 以及方差
以及方差
:
;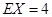 ,
,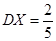
 | 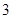 | 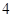 | 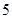 |
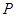 | 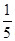 |  | 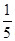 |
;
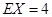 ,
,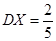
从6个球中取3个球,共有三种情况,三个黄球,两个黄球和一个红球,一个黄球和两个红球,随机变量 的值分别是3,4,5.
的值分别是3,4,5. 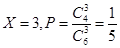 ,同理求出另两个值对应的概率,列出分布列,由公式求出期望
,同理求出另两个值对应的概率,列出分布列,由公式求出期望 以及方差
以及方差 .
.
 的值分别是3,4,5.
的值分别是3,4,5. 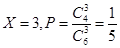 ,同理求出另两个值对应的概率,列出分布列,由公式求出期望
,同理求出另两个值对应的概率,列出分布列,由公式求出期望 以及方差
以及方差 .
.
练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 两个项目,投资
两个项目,投资 项目
项目 万元,一年后获得的利润为随机变量
万元,一年后获得的利润为随机变量 (万元),根据市场分析,
(万元),根据市场分析,
 项目
项目 (万元)与
(万元)与 次独立的调整,且在每次调整中价格下调的概率都是
次独立的调整,且在每次调整中价格下调的概率都是 .
.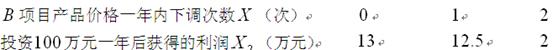
 ;
; ,根据投资获得利润的差异,你愿意选择投资哪个项目?
,根据投资获得利润的差异,你愿意选择投资哪个项目? ).
). 中任选出两位同学,共同帮助成绩在
中任选出两位同学,共同帮助成绩在 中的某一个同学,试列出所有基本事件;若
中的某一个同学,试列出所有基本事件;若 同学成绩为43分,
同学成绩为43分, 同学成绩为95分,求
同学成绩为95分,求 分,负者得
分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多 分或打满
分或打满 局时停止.设甲在每局中获胜的概率为
局时停止.设甲在每局中获胜的概率为 ,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为 .
. 的值;
的值; 表示比赛停止时比赛的局数,求随机变量
表示比赛停止时比赛的局数,求随机变量 .
. 的分布表如表所示,则
的分布表如表所示,则 ▲ .
▲ .
 ,且
,且 ,则实数
,则实数 的值为 ( )
的值为 ( ) ,则随机变量
,则随机变量