题目内容
设函数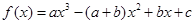 其中
其中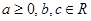
(1)若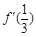 =0,求
=0,求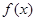 的单调区间;
的单调区间;
(2)设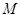 表示
表示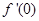 与
与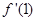 两个数中的最大值,求证:当0≤x≤1时,|
两个数中的最大值,求证:当0≤x≤1时,|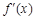 |≤
|≤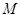 .
.
(1),函数f(x)的单调增区间是(-∞,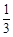 )及(1,+∞) .单调减区间是
)及(1,+∞) .单调减区间是
(2)根据导数判定单调性,进而得到最值,然后来证明结论。
解析试题分析:解:(1)由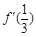 =0,得a=b.
=0,得a=b.
当 时,则
时,则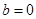 ,
,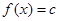 不具备单调性 ..2分
不具备单调性 ..2分
故f(x)= ax3-2ax2+ax+c.
由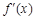 =a(3x2-4x+1)=0,得x1=
=a(3x2-4x+1)=0,得x1=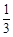 ,x2=1. 3分
,x2=1. 3分
列表:
由表可得,函数f(x)的单调增区间是(-∞,x (-∞, 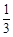 )
)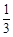
( 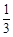 ,1)
,1)1 (1,+∞) 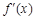
+ 0 - 0 + f(x) 增 极大值 减 极小值 增 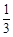 )及(1,+∞) .单调减区间是
)及(1,+∞) .单调减区间是 …5分
…5分
(2)当 时,
时,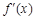 =
=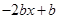
若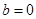
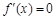 ,
,
若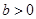 ,或
,或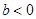 ,
,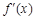 在
在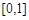 是单调函数,
是单调函数, ≤
≤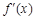 ≤
≤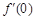 ,或
,或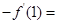
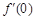 ≤
≤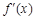 ≤
≤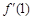 7分
7分
所以,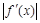 ≤
≤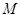
当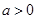 时,
时,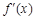 =3ax2-2(a+b)x+b=3
=3ax2-2(a+b)x+b=3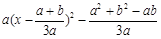 .
.
①当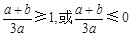 时,则
时,则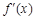 在
在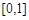 上是单调函数,
上是单调函数,
所以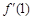 ≤
≤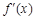 ≤
≤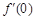 ,或
,或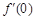 ≤
≤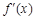 ≤<
≤<

练习册系列答案
相关题目

 的大小关系;
的大小关系; 和
和 是否存在公切线,若存在,求出公切线方程,若不存在,说明理由;
是否存在公切线,若存在,求出公切线方程,若不存在,说明理由; 的大小,并写出判断过程.
的大小,并写出判断过程.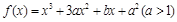 在
在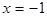 时有极值0。
时有极值0。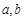 的值;
的值;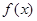 的单调区间。
的单调区间。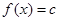 在区间[-4,0]上有三个不同的实根时实数
在区间[-4,0]上有三个不同的实根时实数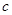 的范围。
的范围。
 在点
在点 处的切线与直线
处的切线与直线 平行,求出这条切线的方程;
平行,求出这条切线的方程; ,讨论函数
,讨论函数 的单调区间;
的单调区间; ,恒有
,恒有 ,求实数
,求实数 的取值范围.
的取值范围.
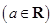 .
.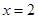 为
为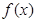 的极值点,求实数
的极值点,求实数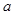 的值;
的值;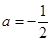 时,方程
时,方程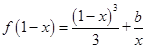 有实根,求实数
有实根,求实数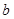 的最大值。
的最大值。 ,是否存在实数
,是否存在实数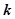 ,使函数在
,使函数在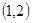 上递减,在
上递减,在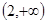 上递增?若存在,求出所有
上递增?若存在,求出所有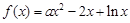 .
.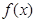 无极值点,但其导函数
无极值点,但其导函数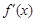 有零点,求
有零点,求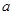 的值;
的值;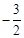 .
.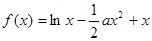
 时,求
时,求 的最大值;
的最大值;
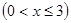 ,以其图象上任意一点
,以其图象上任意一点 为切点的切线的斜率
为切点的切线的斜率 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 时,方程
时,方程 有唯一实数解,求正数
有唯一实数解,求正数 的值.
的值. 与
与 ,
, ,
, 所围成的平面图形的面积。
所围成的平面图形的面积。