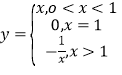题目内容
【题目】如图,在几何体中,四边形![]() 为菱形,对角线
为菱形,对角线![]() 与
与![]() 的交点为
的交点为![]() ,四边形
,四边形![]() 为梯形,
为梯形, ![]() .
.
(Ⅰ)若![]() ,求证:
,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)若![]() ,
, ![]() ,
, ![]() ,求
,求![]() 与平面
与平面![]() 所成角.
所成角.
【答案】(I)证明见解析;(II)证明见解析;(III)![]() .
.
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,证明
,证明![]() 为平行四边形,可得
为平行四边形,可得![]() ,利用线面平行的判定定理即可证明
,利用线面平行的判定定理即可证明![]() 平面
平面![]() ;(2)先证明
;(2)先证明![]() ,
, ![]() ,可证明
,可证明![]() 平面
平面![]() ,从而可证明平面
,从而可证明平面![]() 平面
平面![]() ;(3)做
;(3)做![]() 于
于![]() 为
为![]() 与平面
与平面![]() 所成角,根据余弦定理及等腰三角形性质即可求
所成角,根据余弦定理及等腰三角形性质即可求![]() 与平面
与平面![]() 所成角.
所成角.
试题解析:(Ⅰ)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() .
.
∵对角线![]() 与
与![]() 的交点为
的交点为![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ;
;
(Ⅱ)证明:∵四边形![]() 为菱形,
为菱形,
∴![]() ,
,
∵![]() ,
, ![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ;
;
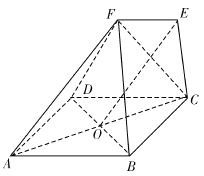
(Ⅲ)
作![]() 于
于![]() .
.
∵平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() 为
为![]() 与平面
与平面![]() 所成角,
所成角,
由题意, ![]() 为正三角形,
为正三角形, ![]() ,
,
∵![]() ,
,
∴![]() 为正三角形,∴
为正三角形,∴![]() .
.
![]() 中,由余弦定理可得
中,由余弦定理可得![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 与平面
与平面![]() 所成角
所成角![]() .
.
【方法点晴】本题主要考查线面平行的判定定理、直线和平面成的角的定义及求法、线面垂直的判定定理以及面面垂直的判定定理,属于中档题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(Ⅰ)是就是利用方法①证明的.

练习册系列答案
相关题目