题目内容
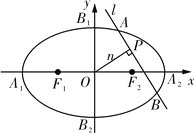
【题目】已知两点![]() 及
及![]() ,点
,点![]() 在以
在以![]() 、
、![]() 为焦点的椭圆
为焦点的椭圆![]() 上,且
上,且![]() 、
、![]() 、
、![]() 构成等差数列.
构成等差数列.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设![]() 是过原点的直线,
是过原点的直线,![]() 是与n垂直相交于
是与n垂直相交于![]() 点,与椭圆相交于
点,与椭圆相交于![]() 两点的直线,
两点的直线,![]() ,是否存在上述直线
,是否存在上述直线![]() 使
使![]() 成立?若存在,求出直线
成立?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(1)![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】试题分析:(Ⅰ)由![]() 构成等差数列可得,
构成等差数列可得, ![]() ,
,![]() .又
.又![]() ,
,![]() ,从而可得结果;(Ⅱ)先证明当
,从而可得结果;(Ⅱ)先证明当![]() 与
与![]() 轴垂直时,不合题意,当
轴垂直时,不合题意,当![]() 与x轴不垂直时,设
与x轴不垂直时,设![]() 的方程为
的方程为![]() ,由
,由![]() 与
与![]() 垂直相交于
垂直相交于![]() 点且
点且![]() ,得
,得![]() ,利用韦达定理以及平面向量数量积公式,可得
,利用韦达定理以及平面向量数量积公式,可得![]() ,矛盾,故此时的直线
,矛盾,故此时的直线![]() 也不存在.
也不存在.
.试题解析:(Ⅰ)依题意,设椭圆![]() 的方程为
的方程为![]() .
.
![]()
![]() 构成等差数列,
构成等差数列,
![]()
![]() ,
,![]() .
.
又![]() ,
,![]() .
.
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)设![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,
,
假设存在直线![]() 使
使![]() 成立,
成立,
(ⅰ)当![]() 与
与![]() 轴垂直时,满足
轴垂直时,满足![]() 的直线
的直线![]() 的方程为
的方程为![]() 或
或![]()
当![]() 时,
时,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() .
.
∴![]()
当![]() 时,同理可得
时,同理可得![]() ,
,
即此时的直线![]() 不存在.
不存在.
(ⅱ)当![]() 与
与![]() 轴不垂直时,设
轴不垂直时,设![]() 的方程为
的方程为![]() ,
,
由![]() 与
与![]() 垂直相交于
垂直相交于![]() 点且
点且![]() ,得
,得![]() .
.
因为![]() ,
,![]() ,
,
![]() ,
,![]() .
.
将![]() 代入椭圆方程,得
代入椭圆方程,得![]()
由根与系数的关系得:![]()
![]() ,
,
![]()
即![]() ,矛盾,故此时的直线
,矛盾,故此时的直线![]() 也不存在.
也不存在.
综上可知,使![]() 成立的直线
成立的直线![]() 不存在.
不存在.

练习册系列答案
相关题目
【题目】为了解某地区某种农产品的年产量![]() (单位:吨)对价格
(单位:吨)对价格![]() (单位:千元/吨)和利润
(单位:千元/吨)和利润![]() 的影响,对近五年该农产品的年产量和价格统计如下表:
的影响,对近五年该农产品的年产量和价格统计如下表:
| 1 | 2 | 3 | 4 | 5 |
| 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
已知![]() 和
和![]() 具有线性相关关系.
具有线性相关关系.
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)若每吨该农产品的成本为2千元,假设该农产品可全部卖出,预测当年产量为多少吨时,年利润![]() 取到最大值?(保留一位小数)
取到最大值?(保留一位小数)
参考数据及公式: ![]() ,
, ![]() ,
,

 ,
, ![]() .
.