[题目]已知抛物线: 的焦点为.准线为.三个点. . 中恰有两个点在上．(1)求抛物线的标准方程,(2)过的直线交于. 两点.点为上任意一点.证明:直线. . 的斜率成等差数列．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知抛物线：的焦点为，准线为，三个点，，中恰有两个点在上．

（1）求抛物线的标准方程；

（2）过的直线交于，两点，点为上任意一点，证明：直线，，的斜率成等差数列．

【答案】(1) (2)见解析

【解析】试题分析：（1）由对称关系可知，两点在上，求得抛物线的标准方程为；（2）设直线的方程为，联立抛物线方程，得到韦达定理，表示出直线的斜率，证明满足等差中项公式即可。

试题解析：

（I）因为抛物线：关于x轴对称，

所以中只能是两点在上，

带入坐标易得，所以抛物线的标准方程为

（II）证明：抛物线的焦点的坐标为，准线的方程为.

设直线的方程为， .

由，可得，所以，

于是，

设直线的斜率分别为，

一方面，

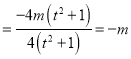另一方面， .

所以，即直线的斜率成等差数列

练习册系列答案

(1)求成绩在的频率；

(2)根据频率分布直方图算出样本数据平均数；

(3)为了分析成绩与班级、学校等方面的关系，必须按成绩再从这10000人中用分层抽样方法抽出20人作进一步分析，则成绩在的这段应抽多少人？

【题目】为了解某地区某种农产品的年产量（单位：吨）对价格（单位：千元/吨）和利润的影响，对近五年该农产品的年产量和价格统计如下表：

	1	2	3	4	5
	7.0	6.5	5.5	3.8	2.2

已知和具有线性相关关系.

（Ⅰ）求关于的线性回归方程；

（Ⅱ）若每吨该农产品的成本为2千元，假设该农产品可全部卖出，预测当年产量为多少吨时，年利润取到最大值？（保留一位小数）

参考数据及公式：，，

， .

【题目】如图，在几何体中，四边形为菱形，对角线与的交点为，四边形为梯形， .

（Ⅰ）若，求证：平面；

（Ⅱ）求证：平面平面；

（Ⅲ）若，，，求与平面所成角.

【题目】已知函数.

（1）讨论函数的单调性；

（2）当时，记函数的极小值为，若恒成立，求满足条件的最小整数.

【题目】在平面直角坐标系中，的两个顶点的坐标分别为，三个内角满足.

（1）若顶点的轨迹为，求曲线的方程；

（2）若点为曲线上的一点，过点作曲线的切线交圆于不同的两点（其中在的右侧），求四边形面积的最大值.

【题目】设椭圆的离心率为，且过点.

（1）求椭圆的方程；

（2）是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆恒有两个交点，且（为坐标原点）？若存在，写出该圆的方程；若不存在，说明理由.

【题目】已知关于的一元二次方程，其中。

（I）若随机选自集合，随机选自集合，求方程有实根的概率;

（Ⅱ）若随机选自区间，随机选自区间，求方程有实根的概率。

【题目】已知AF平面ABCD，四边形ABEF为矩形，四边形ABCD为直角梯形， .

（1）求证：平面；

（2）线段上是否存在一点，使得 ?若存在，确定点的位置；若不存在，请说明理由．

试题分类