Question

【题目】具有性质：的函数，我们称为满足“倒负”变换的函数。给出下列函数：

① ② ③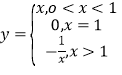 其中满足“倒负”变换的函数是()

A. ①② B. ①③ C. ②③ D. ①

Answer 1

【答案】C

【解析】

利用题中的新定义，对各个函数进行判断是否具有f（）=﹣f（x），判断出是否满足“倒负”变换，即可得答案．

①f（）=ln=ln≠﹣f（x），

不满足“倒负”变换的函数；

②f（）===﹣=﹣f（x），

满足“倒负”变换的函数；

对于③，当0＜x＜1时，＞1，f（x）=x，f（）=﹣x=﹣f（x）；

当x＞1时，0＜＜1，f（x）=﹣，f（）=﹣f（x）；

当x=1时，=1，f（x）=0，f（）=f（1）=0=﹣f（x），

满足“倒负”变换的函数；

综上：②③是符合要求的函数；

故选：C．