��Ŀ����
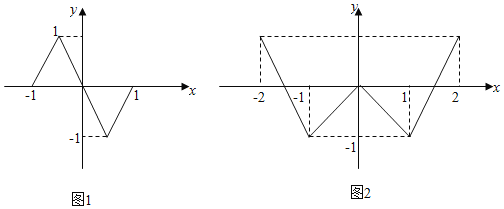
����Ŀ������������פ���У���ɫ��������ʱ��.ij����ͳ��������ʾ��2017����й��������û�����ǼǷֲ���ͼ1��ʾ��һ��������ʹ�õ�����Ƶ�ʷֲ�����ͼ��ͼ2��ʾ.�������������û����������Ϊ�������ˡ���20����39�꣩�͡��������ˡ���19�꼰���»���40�꼰���ϣ����࣬��һ����ʹ�õĴ���Ϊ6�λ�6�����ϵij�Ϊ������ʹ�õ����û�����ʹ�ô���Ϊ5�λ���5�εij�Ϊ������ʹ�õ����û�������֪�ڡ�����ʹ�õ����û�������![]() �ǡ������ˡ���
�ǡ������ˡ���

��1���ֶԸ���������С�����ʹ�ù��������������ϵ���ĵ��飬������������ķ�������ȡһ������Ϊ200���������������ͼ���е����ݣ���ȫ����![]() ���������������������Ķ����Լ��飬�ж����ж����տ�����Ϊ����ʹ�ù��������������йأ�
���������������������Ķ����Լ��飬�ж����ж����տ�����Ϊ����ʹ�ù��������������йأ�

��2����Ƶ����Ϊ���ʣ����Ӹ��������������ȡ3�ˣ������о���ʹ�ù��������ġ��������ˡ�����Ϊ�������![]() ����
����![]() �ķֲ�������.
�ķֲ�������.
���ο����ݣ������Լ����ֵ�� ������
������![]() ��
��

���𰸡�(1) ��85%�İ��տ�����Ϊ����ʹ�ù��������������й�;(2)������.
�������������������1�����ݹ��������û�����ȼ۷ֲ��������ݣ��ɲ�ȫ����![]() �����������ù�ʽ�ɵ�
�����������ù�ʽ�ɵ�![]()
![]() ���Ӷ��ɵ���85%�İ��տ�����Ϊ����ʹ�ù��������������й�����2��
���Ӷ��ɵ���85%�İ��տ�����Ϊ����ʹ�ù��������������й�����2��![]() �Ŀ���ȡֵΪ
�Ŀ���ȡֵΪ![]() �����ݶ����¼����ʹ�ʽ��������������Ӧ�ĸ��ʣ��Ӷ��ɵ÷ֲ��У���������������ʽ�ɵ�
�����ݶ����¼����ʹ�ʽ��������������Ӧ�ĸ��ʣ��Ӷ��ɵ÷ֲ��У���������������ʽ�ɵ�![]() ����ѧ����..
����ѧ����..
�����������1����ȫ�����������£�
������ | �������� | �ϼ� | |
����ʹ�ù������� | 100 | 20 | 120 |
����ʹ�ù������� | 60 | 20 | 80 |
�ϼ� | 160 | 40 | 200 |
����![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
��![]()
![]() ��
��
����85%�İ��տ�����Ϊ����ʹ�ù��������������й�.
��2���ɣ�1������������֪������ʹ�ù��������ġ��������ˡ�ռ����������Ƶ��Ϊ![]() �����ڳ�ȡ���û��г��־���ʹ�õ����ġ��������ˡ��ĸ���Ϊ0.1��
�����ڳ�ȡ���û��г��־���ʹ�õ����ġ��������ˡ��ĸ���Ϊ0.1��
��![]() ��
�� ![]()
![]()
![]() ��
��
��![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 0 | 1 | 2 | 3 |
| 0.729 | 0.243 | 0.027 | 0.001 |
��![]() ����ѧ����
����ѧ����![]()

 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д� ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д�����Ŀ��Ϊ�˽�ij����ij��ũ��Ʒ�������![]() ����λ���֣��Լ۸�
����λ���֣��Լ۸�![]() ����λ��ǧԪ/�֣�������
����λ��ǧԪ/�֣�������![]() ��Ӱ�죬�Խ������ũ��Ʒ��������ͼ۸�ͳ�����±���
��Ӱ�죬�Խ������ũ��Ʒ��������ͼ۸�ͳ�����±���
| 1 | 2 | 3 | 4 | 5 |
| 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
��֪![]() ��
��![]() ����������ع�ϵ.
����������ع�ϵ.
������![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]() ��
��
������ÿ�ָ�ũ��Ʒ�ijɱ�Ϊ2ǧԪ�������ũ��Ʒ��ȫ��������Ԥ������Ϊ���ٶ�ʱ��������![]() ȡ�����ֵ��������һλС����
ȡ�����ֵ��������һλС����
�ο����ݼ���ʽ�� ![]() ��
�� ![]() ��
��

 ��
�� ![]() .
.