题目内容
已知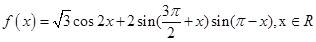
(1)最小正周期及对称轴方程;
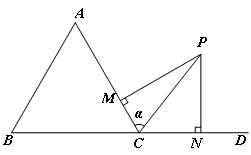
(2)已知锐角 的内角
的内角 的对边分别为
的对边分别为 ,且
,且  ,
, ,求
,求 边上的高的最大值.
边上的高的最大值.
(1)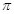
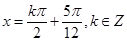 (2)
(2)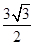
解析试题分析:(1)f(x)解析式利用二倍角的正弦、诱导公式化简,整理后再利用两角和与差的正弦函数公式化为一个角的正弦函数,代入周期公式即可求出f(x)的最小正周期,根据正弦函数的对称性即可确定出对称轴方程;
(2)由 ,根据第一问确定出的f(x)解析式,求出A的度数,利用余弦定理列出关系式,利用基本不等式求出bc的最小值,将sinA,bc的最小值代入三角形面积公式求出△ABC的面积,然后在求出h的最大值即可.
,根据第一问确定出的f(x)解析式,求出A的度数,利用余弦定理列出关系式,利用基本不等式求出bc的最小值,将sinA,bc的最小值代入三角形面积公式求出△ABC的面积,然后在求出h的最大值即可.
(1)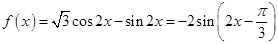
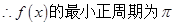

(2)由 得
得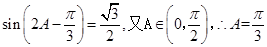
由余弦定理得
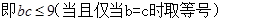
设 边上的高为
边上的高为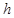 ,由三角形等面积法知
,由三角形等面积法知
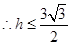 ,即
,即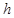 的最大值为
的最大值为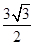
考点:1.余弦定理;2.正弦函数的对称性和周期;2.基本不等式的运用.

练习册系列答案
相关题目
 )(ω>0)的最小正周期为π.
)(ω>0)的最小正周期为π. ]上的单调性.
]上的单调性. 0,
0, .
. 值; (2)求
值; (2)求 的值.
的值.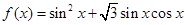 .
. 的值;
的值;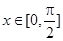 时,求函数
时,求函数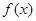 的最大值和最小值.
的最大值和最小值. ,函数
,函数 .
.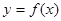 的周期和对称轴方程;
的周期和对称轴方程;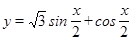 的图像,并说明这个图像是由
的图像,并说明这个图像是由 的图像经过怎样的变换得到的.
的图像经过怎样的变换得到的.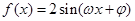
 的图形向右平移
的图形向右平移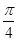 个单位后得到
个单位后得到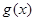 的图像,已知
的图像,已知 ,与x轴相交于点P、Q,点M为最高点,且
,与x轴相交于点P、Q,点M为最高点,且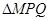 的面积为
的面积为 .
.
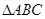 中,
中,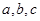 分别是角A,B,C的对边,
分别是角A,B,C的对边, ,且
,且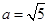 ,求
,求 ,
,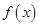 并求
并求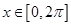 时,求f(x)的最小值以及取得最小值时x的集合.
时,求f(x)的最小值以及取得最小值时x的集合. ,acosA=bcosB.
,acosA=bcosB.