题目内容
将函数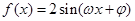
 的图形向右平移
的图形向右平移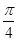 个单位后得到
个单位后得到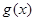 的图像,已知
的图像,已知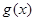 的部分图像如图所示,该图像与y轴相交于点
的部分图像如图所示,该图像与y轴相交于点 ,与x轴相交于点P、Q,点M为最高点,且
,与x轴相交于点P、Q,点M为最高点,且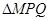 的面积为
的面积为 .
.
(1)求函数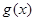 的解析式;
的解析式;
(2)在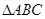 中,
中,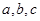 分别是角A,B,C的对边,
分别是角A,B,C的对边, ,且
,且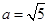 ,求
,求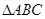 面积的最大值.
面积的最大值.
(1) ;(2)
;(2)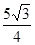 .
.
解析试题分析:本题主要考查三角函数图象、三角函数图象的平移变换、余弦定理、三角函数面积、基本不等式等基础知识,考查学生的分析问题解决问题的能力、计算能力.第一问,先将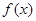 的图象向右平移
的图象向右平移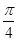 个单位得到
个单位得到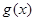 的解析式,由解析式得最大值M=2,利用三角形面积公式可得到
的解析式,由解析式得最大值M=2,利用三角形面积公式可得到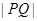 ,而周期
,而周期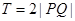 ,利用周期的计算公式得到
,利用周期的计算公式得到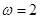 ,又因为
,又因为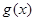 过
过 ,代入解析式得到
,代入解析式得到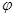 的值,从而得到
的值,从而得到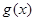 的解析式;第二问,先利用
的解析式;第二问,先利用 ,利用特殊角的三角函数值得到角A的大小,再利用余弦定理得到b和c的一个关系式,利用基本不等式得到
,利用特殊角的三角函数值得到角A的大小,再利用余弦定理得到b和c的一个关系式,利用基本不等式得到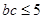 ,代入到三角形面积公式中,得到面积的最大值.
,代入到三角形面积公式中,得到面积的最大值.
(1)由题意可知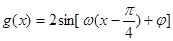
由于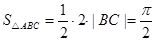 ,则
,则 ,∴
,∴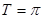 ,即
,即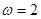 2分
2分
又由于 ,且
,且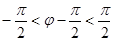 ,则
,则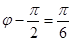 ,∴
,∴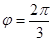 5分
5分
即 . 6分
. 6分
(2)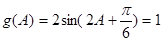 ,
,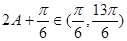 则
则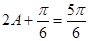 ,∴
,∴ 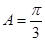 8分
8分
由余弦定理得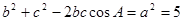 ,∴
,∴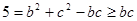 10分
10分
∴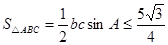 ,当且仅当
,当且仅当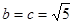 时,等号成立,故
时,等号成立,故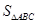 的最大值为
的最大值为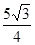 . 12分
. 12分
考点:三角函数图象、三角函数图象的平移变换、余弦定理、三角函数面积、基本不等式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 直线
直线 是
是 图像的任意两条对称轴,且
图像的任意两条对称轴,且 的最小值为
的最小值为 .
. 的单调增区间;
的单调增区间; 的
的 的取值范围.
的取值范围. 求
求 的值;
的值;
 的内角
的内角 的对边分别为
的对边分别为 ,且
,且  ,
, ,求
,求 边上的高的最大值.
边上的高的最大值.
 .
.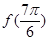 的值;
的值;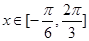 时,求
时,求 .
.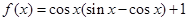 .
. 的最小正周期;
的最小正周期;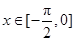 时,求函数
时,求函数 的部分图象如图所示.
的部分图象如图所示.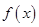 的解析式,并写出
的解析式,并写出 的内角分别是A,B,C,角A为锐角,且
的内角分别是A,B,C,角A为锐角,且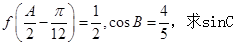 的值.
的值.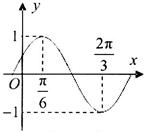
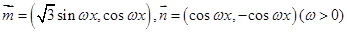 ,函数
,函数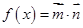 的最小正周期为
的最小正周期为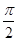 .
.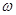 的值;
的值;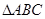 的三边
的三边 、
、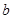 、
、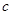 满足:
满足: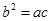 ,且边
,且边 ,若关于
,若关于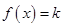 有两个不同的实数解,求实数
有两个不同的实数解,求实数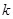 的取值范围.
的取值范围.