题目内容
19.给出命题:(1)垂直于同一直线的两个平面平行;
(2)平行于同一直线的两个平面平行;
(3)平行于两相交平面的直线一定平行于这两相交平面的交线;
(4)平行于同一平面的两个平面平行;
其中正确命题个数有( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由空间平面与平面平行的判定与性质定理,可以很容易得出答案.
解答 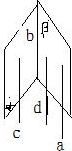 解:(1)垂直于同一直线的两个平面平行,关键平面与平面平行的判定定理可知正确;
解:(1)垂直于同一直线的两个平面平行,关键平面与平面平行的判定定理可知正确;
(2)平行于同一直线的两个平面平行或相交,故不正确;
(3)由a∥α得,经过a的平面与α相交于直线c,则a∥c,
同理,设经过a的平面与β相交于直线d,则a∥d,由平行公理得:c∥d,
则c∥β,又c?α,α∩β=b,所以c∥b,又a∥c,所以a∥b,故正确;
(4)平行于同一平面的两个平面平行,正确.
故选:C.
点评 本题考查空间平面与平面的位置关系,考查平面与平面平行的判定与性质,属基础题

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
9.已知$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$、$\overrightarrow{{e}_{3}}$均为单位向量,其中任何两个向量的夹角均为120°,则|$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$+$\overrightarrow{{e}_{3}}$|=( )
| A. | 3 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 0 |
10.以抛物线y=$\frac{1}{4}$x2的焦点为圆心,且过坐标原点的圆的方程为( )
| A. | x2+y2-x=0 | B. | x2+y2-2x=0 | C. | x2+y2-y=0 | D. | x2+y2-2y=0 |
4.若(1-2x)9=a0+a1x+a2x2+…+a8x8+a9x9,则a1+a2+…+a8的值为( )
| A. | -1 | B. | -2 | C. | -512 | D. | 510 |
9.a,b∈R,下列结论成立的是( )
| A. | 若a<b,则ac<bc | B. | 若a<b,c<d,则ac<bd | ||
| C. | 若a<b,则a-c<b-c | D. | 若a<b,则an<bn(n∈N*,n≥2) |