题目内容
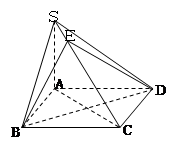
若P为棱长为1的正四面体内的任一点,则它到这个正四面体各面的距离之和为______.
A.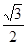 | B.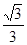 | C.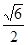 | D.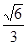 |
D
解:因为正四面体的体积等于四个三棱锥的体积和,设它到四个面的距离分别为a,b,c,d,由于是棱长为1的正四面体,故四个面的面积都是一样的,且为
 ,由顶点到底面的投影在地底面的中心,此点到三个顶点的距离都是高的2/3,高为
,由顶点到底面的投影在地底面的中心,此点到三个顶点的距离都是高的2/3,高为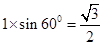 ,故底面中心到底面顶点的距离都是
,故底面中心到底面顶点的距离都是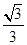 ,由此知道顶点到底面的距离为
,由此知道顶点到底面的距离为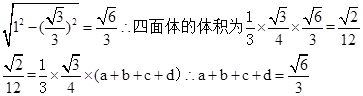
 ,由顶点到底面的投影在地底面的中心,此点到三个顶点的距离都是高的2/3,高为
,由顶点到底面的投影在地底面的中心,此点到三个顶点的距离都是高的2/3,高为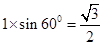 ,故底面中心到底面顶点的距离都是
,故底面中心到底面顶点的距离都是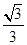 ,由此知道顶点到底面的距离为
,由此知道顶点到底面的距离为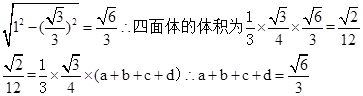

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的棱长都为2,
的棱长都为2, 为
为 的中点,则
的中点,则 与面GEF成角的正弦值是( )
与面GEF成角的正弦值是( )




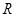 ,则此四面体的棱长为( )
,则此四面体的棱长为( )


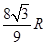

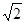 π
π

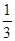 B、
B、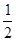 C、
C、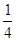 D、1
D、1 是边长为1的正方形,
是边长为1的正方形,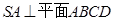 ,
,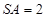 ,E是侧棱SC上的一点.
,E是侧棱SC上的一点.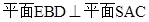 ;
;