题目内容
(本题满分10分)
已知某个几何体的三视图如图(主视图的弧线是半圆),根据图中标出的数据:
⑴求这个组合体的表面积;
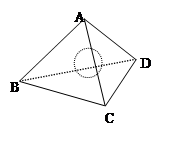
⑵若组合体的底部几何体记为ABCD-A1B1C1D1,如图,其中A1B1BA为正方形.
①求证:A1B⊥平面AB1C1D;
②若P为棱A1B1上一点,求AP+PC1的最小值.


已知某个几何体的三视图如图(主视图的弧线是半圆),根据图中标出的数据:
⑴求这个组合体的表面积;
⑵若组合体的底部几何体记为ABCD-A1B1C1D1,如图,其中A1B1BA为正方形.
①求证:A1B⊥平面AB1C1D;
②若P为棱A1B1上一点,求AP+PC1的最小值.


解:⑴此组合体的下部为长方体,上部为半个圆柱:
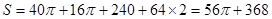 -----4分
-----4分
⑵①在长方体中,AD⊥面A1B1BA,
又A1B 面A1B1BA,所以AD⊥A1B,
面A1B1BA,所以AD⊥A1B,
又A1B1BA是边长为8的正方形,
所以A1B⊥AB1,而AB1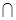 AD=A,
AD=A,
所以A1B⊥面AB1C1D.----------7分
②将上底面展开,与面A1B1BA共面时,
连结C1A交A1B1于点P,即AC1为最
短距离. 此时长度为 --------------------------10分.
--------------------------10分.
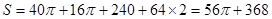 -----4分
-----4分⑵①在长方体中,AD⊥面A1B1BA,
又A1B
 面A1B1BA,所以AD⊥A1B,
面A1B1BA,所以AD⊥A1B,又A1B1BA是边长为8的正方形,
所以A1B⊥AB1,而AB1
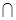 AD=A,
AD=A,所以A1B⊥面AB1C1D.----------7分
②将上底面展开,与面A1B1BA共面时,
连结C1A交A1B1于点P,即AC1为最
短距离. 此时长度为
 --------------------------10分.
--------------------------10分.略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
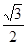
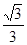
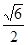
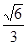
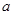 平方米,且它的侧面展开图是一个半圆,则这个圆锥的底面的直径为__________________________
平方米,且它的侧面展开图是一个半圆,则这个圆锥的底面的直径为__________________________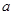 的正方体外接球的表面积为
的正方体外接球的表面积为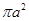
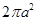
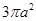
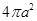
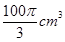
 ,那么两个球的半径之比为( )
,那么两个球的半径之比为( )
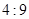

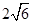 ,此三棱锥内有一个球和四个面都相切.
,此三棱锥内有一个球和四个面都相切.