题目内容
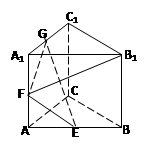
正三棱柱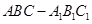
的棱长都为2，
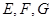为
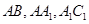的中点，则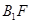
与面GEF成角的正弦值是（ ）
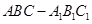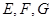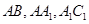的棱长都为2，为的中点，则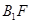与面GEF成角的正弦值是（ ）A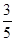． | B． |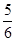
C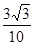． | D． |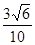
A
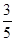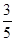解 :利用等体积，计算B1到平面EFG距离，再利用正弦函数，可求B1F 与面GEF成角的正弦值为，选A
，选A
练习册系列答案
名校课堂系列答案
相关题目
名校课堂系列答案题目内容
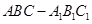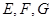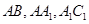的棱长都为2，为的中点，则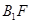与面GEF成角的正弦值是（ ）| A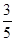． | B． |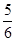
| C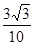． | D． |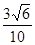
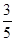，选A名校课堂系列答案
中，底面
是直角梯形，
，
，
，
，
平面
．
平面
；
平面
； 
是
的中点，求三棱锥
的体积．
，AB为直径，C是圆周上一点，且
，平面
平面
，
，
，
，设直线PC与平面
、
的大小为
，则
