题目内容
【题目】如图,长方体ABCD﹣A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1 , D1C1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形. 
(I)在图中画出这个正方形(不必说明画法和理由);
(II)求直线AF与平面α所成角的正弦值.
【答案】解:(I)交线围成的正方形EFGH如图:(II)作EM⊥AB,垂足为M,则:
EH=EF=BC=10,EM=AA1=8;
∴ ![]() ,∴AH=10;
,∴AH=10;
以边DA,DC,DD1所在直线为x,y,z轴,建立如图所示空间直角坐标系,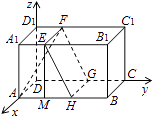
则:A(10,0,0),H(10,10,0),E(10,4,8),F(0,4,8);
∴ ![]() ;
;
设 ![]() 为平面EFGH的法向量,则:
为平面EFGH的法向量,则: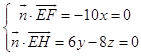 ,取z=3,则
,取z=3,则 ![]() ;
;
若设直线AF和平面EFGH所成的角为θ,则:
sinθ= ![]() =
= ![]() ;
;
∴直线AF与平面α所成角的正弦值为 ![]()
【解析】(I)容易知道所围成正方形的边长为10,再结合长方体各边的长度,即可找出正方形的位置,从而画出这个正方形;(II)分别以直线DA,DC,DD1为x,y,z轴,建立空间直角坐标系,考虑用空间向量解决本问,能够确定A,H,E,F几点的坐标.设平面EFGH的法向量为 ![]() ,根据
,根据 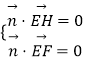 即可求出法向量
即可求出法向量 ![]() ,
, ![]() 坐标可以求出,可设直线AF与平面EFGH所成角为θ,由sinθ=
坐标可以求出,可设直线AF与平面EFGH所成角为θ,由sinθ= ![]() 即可求得直线AF与平面α所成角的正弦值.
即可求得直线AF与平面α所成角的正弦值.
【考点精析】解答此题的关键在于理解空间角的异面直线所成的角的相关知识,掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则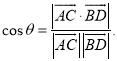 .
.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目