题目内容
13.求π的近似值可用如下公式$\frac{π}{6}$=$\frac{1}{{1}^{2}}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{n}^{2}}$,直到第n项的值小于0.00001为止,最后一项不计入求和,然后求π的近似值,写出程序,并画出程序框图.分析 可以先将$\frac{1}{{1}^{2}}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{n}^{2}}$逐项累加,然后用其和sum乘以6,再开方即可,要注意循环终止条件的作用.
解答 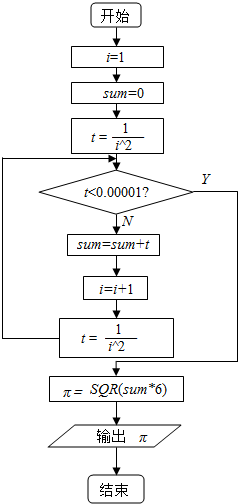 解:程序如下:
解:程序如下:
i=1
sum=0
t=1/i^2
WHILE t>=0.00001
sum=sum+t
i=i+1
t=1/i^2
WEND
π=SQR(sum*6)
PRINT“π=“:π
END
框图如右图所示:
点评 本题主要考查设计程序框图解决实际问题.在一些算法中,也经常会出现从某处开始,按照一定条件,反复执行某一处理步骤的情况,这就是循环结构.循环结构要在某个条件下终止循环,这就需要条件分支结构来判断.在循环结构中都有一个计数变量和累加变量.计数变量用于记录循环次数,累加变量用于输出结果,计数变量和累加变量一般是同步执行的,累加一次,计数一次.

练习册系列答案
相关题目
3.过点P(1,2)作圆(x+1)2+(y+1)2=1的两条切线,切点分别为A,B,则$\overrightarrow{PA}$•$\overrightarrow{PB}$=( )
| A. | $\frac{121}{12}$ | B. | $\frac{125}{12}$ | C. | $\frac{131}{13}$ | D. | $\frac{132}{13}$ |
 一船向正北航行,到达B处时,看见正西方向有相距10海里的两个灯塔C、D恰好与它在一条直线上,继续航行1小时后到达A处,看见一灯塔在船的南偏西60°方向,另一灯塔在船的南偏西75°方向(如图所示),则这只船的速度是5海里/小时.
一船向正北航行,到达B处时,看见正西方向有相距10海里的两个灯塔C、D恰好与它在一条直线上,继续航行1小时后到达A处,看见一灯塔在船的南偏西60°方向,另一灯塔在船的南偏西75°方向(如图所示),则这只船的速度是5海里/小时.