题目内容
【题目】已知：如图，梯形ABCD中，AD∥BC，∠C= 
，以AB为直径的⊙O恰与CD相切于点E，⊙O交BC于F，连结EF． 
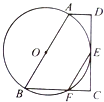
（1）求证：AD+BC=AB；
（2）求证：EF是AD与AB的等比中项．
【答案】
（1）证明：如图所示，
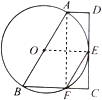
连接OE，∵CD与⊙O相切于点E，
∴OE= 
AB，
又OE⊥DC，
∠C= 
，
∴OE∥BC，且OE= （AD+BC），
∴AD+BC=AB；
（2）证明：∵CD与⊙O相切，
∴CE2=CFCB，
连接AF，则AF⊥BF，
∴AF∥CD，
∴AD=FC，
∴EF2=CE2+CF2
=CFCB+CF2
=CF（CB+CF）
=AD（CB+AD）
=ADAB；
即EF是AD与AB的等比中项
【解析】（1）连接OE，利用圆的直径与梯形的中位线定理，即可证明结论成立；（2）连接AF，利用勾股定理和切割线定理，结合题意即可求出EF是AD与AB的等比中项．
练习册系列答案
相关题目
