题目内容
【题目】已知函数![]() 是定义域为
是定义域为![]() 的奇函数,当
的奇函数,当![]() .
.
(Ⅰ)求出函数![]() 在
在![]() 上的解析式;
上的解析式;
(Ⅱ)在答题卷上画出函数![]() 的图象,并根据图象写出
的图象,并根据图象写出![]() 的单调区间;
的单调区间;

(Ⅲ)若关于![]() 的方程
的方程![]() 有三个不同的解,求
有三个不同的解,求![]() 的取值范围。
的取值范围。
【答案】(Ⅰ) ;(Ⅱ)单调增区间为
;(Ⅱ)单调增区间为![]() ,
,
单调减区间为![]() ;(Ⅲ)
;(Ⅲ) ![]() .
.
【解析】试题分析; (Ⅰ)①由于函数![]() 是定义域为
是定义域为![]() 的奇函数,则
的奇函数,则![]() ;
;
②当![]() 时,
时, ![]() ,因为
,因为![]() 是奇函数,所以
是奇函数,所以![]() ,可得当
,可得当![]() 时
时![]() 的解析式,从而得到
的解析式,从而得到![]() 在
在![]() 上的解析式;
上的解析式;
(Ⅱ)根据(Ⅰ)得到的解析式可画出函数![]() 的图象,进而得到
的图象,进而得到![]() 的单调区间;
的单调区间;
(Ⅲ)由(1)可得![]() 有极大值1,极小值-1,进而可构造关于
有极大值1,极小值-1,进而可构造关于![]() 的不等式,解不等式可得答案.
的不等式,解不等式可得答案.
试题分析;(Ⅰ)①由于函数![]() 是定义域为
是定义域为![]() 的奇函数,则
的奇函数,则![]() ;
;
②当![]() 时,
时, ![]() ,因为
,因为![]() 是奇函数,所以
是奇函数,所以![]() .
.
所以![]() .
.
综上: 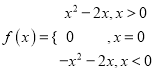
(Ⅱ)图象如图所示.(图像给2分)
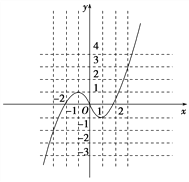
单调增区间: ![]()
单调减区间: ![]()
(Ⅲ)∵方程![]() 有三个不同的解
有三个不同的解
∴![]()
∴![]()

【题目】为了了解初三学生女生身高情况,某中学对初三女生身高进行了一次测量,所得数据整理后列出了频率分布表如下:
组 别 | 频数 | 频率 |
[145.5,149.5) | 1 | 0.02 |
[149.5,153.5) | 4 | 0.08 |
[153.5,157.5) | 20 | 0.40 |
[157.5,161.5) | 15 | 0.30 |
[161.5,165.5) | 8 | 0.16 |
[165.5,169.5) | m | n |
合 计 | M | N |

(1)求出表中![]() 所表示的数;
所表示的数;
(2)画出频率分布直方图;
【题目】某小学为迎接校运动会的到来,在三年级招募了16名男志愿者和14名女志愿者.调查发现,男、女志愿者中分别各有10人和6人喜欢运动,其余人员不喜欢运动.
(1)根据以上数据完成2×2列联表,并说明是否有95%的把握认为性别与喜欢运动有关;
喜欢运动 | 不喜欢运动 | 总计 | |
男 | |||
女 | |||
总计 |
(2)如果喜欢运动的女志愿者中恰有4人懂得医疗救护,现从喜欢运动的女志愿者中抽取2名负责处理应急事件,求抽出的2名志愿者都懂得医疗救护的概率.
附:K2= ,
,
P(K2≥k0) | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 10.828 |