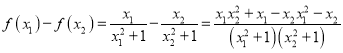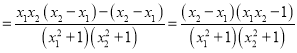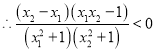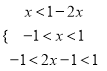��Ŀ����
����Ŀ����֪����![]() .
.
��1���жϲ�֤������![]() ����ż�ԣ�
����ż�ԣ�
��2���жϵ�![]() ʱ����
ʱ����![]() �ĵ����ԣ����ö���֤����
�ĵ����ԣ����ö���֤����
��3����![]() ������Ϊ
������Ϊ![]() ���ⲻ��ʽ
���ⲻ��ʽ![]() .
.
���𰸡���1���溯����2����������3��![]()
�������������������1���ж���֤����������ż�ԣ�����Ҫȷ�������Ķ������Ƿ����ԭ��Գƣ����ж�f(-x)��f(x)�Ĺ�ϵ������Զ������ϵ�����x��������f(-x)=f(x)����ż���������f(-x)=-f(x)�����溯���������Ƿ����ż��������2�������������Զ���֤�������ԣ������裬��������жϣ��½���������衣��3���ɣ�1����2���溯��![]() �ڣ�-1��1��Ϊ����������
�ڣ�-1��1��Ϊ����������
ԭ����ʽ����Ϊf(2x-1)<-f(x),��f(2x-1)<f(-x),���ɺ����ĵ����Լ����壨-1��1������x��Χ��
�����������1������![]() Ϊ�溯����֤�����£�
Ϊ�溯����֤�����£�
![]() ������Ϊ
������Ϊ![]()
��![]()
![]() Ϊ�溯��
Ϊ�溯��
��2������![]() �ڣ�-1��1��Ϊ����������֤�����£�
�ڣ�-1��1��Ϊ����������֤�����£�
��ȡ![]() ����
����


![]()
![]() ��
�� ![]()

��![]()
��![]() �ڣ�-1��1����Ϊ������
�ڣ�-1��1����Ϊ������
��3���ɣ�1������2���ɵ�
![]() ��
��
 ��ã�
��ã� ![]()
���ԣ�ԭ����ʽ�Ľ⼯Ϊ![]()
���㾦��
��1����ż�ԣ��ж���֤����������ż�ԣ�����Ҫȷ�������Ķ������Ƿ����ԭ��Գƣ����ж�f(-x)��f(x)�Ĺ�ϵ������Զ������ϵ�����x��������f(-x)=f(x)����ż���������f(-x)=-f(x)�����溯���������Ƿ����ż������
��2�������ԣ������������Զ���֤�������ԣ������裬��������ţ��½���������衣
�����͡������
��������
22
����Ŀ����֪����![]() .
.
��1����![]() �Ķ������ֵ�����
�Ķ������ֵ�����![]() ����ʵ��
����ʵ��![]() ��ֵ��
��ֵ��
��2����![]() ������
������![]() ���Ǽ��������Ҷ������
���Ǽ��������Ҷ������![]() ������
������![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����![]() ���Ҷ������
���Ҷ������![]() ��������
��������![]() ��ʹ��
��ʹ��![]() ��������ʵ��
��������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
���𰸡���1��![]() ��2��
��2��![]() ��3��
��3��![]()
�������������������1�������ö��κ���������ȷ������![]() �ĵ����ݼ�����Ϊ
�ĵ����ݼ�����Ϊ![]() ����
����![]() ��
��![]() �����ݼ���Ȼ���ɶ�������ֵ���г���ʽ��ϵ���Ӷ���⼴�ɣ���2���ɣ�1����֪
�����ݼ���Ȼ���ɶ�������ֵ���г���ʽ��ϵ���Ӷ���⼴�ɣ���2���ɣ�1����֪![]() ������ȷ��
������ȷ��![]() ��ȡֵ��Χ
��ȡֵ��Χ![]() ��Ȼ��ȷ��
��Ȼ��ȷ��![]() ʱ����
ʱ����![]() �����ֵ
�����ֵ![]() ��������ⲻ��ʽ��
��������ⲻ��ʽ��![]() ���ɣ���3�������������
���ɣ���3�������������![]() ��������
��������![]() ��ʹ��
��ʹ��![]() ������ת��Ϊ
������ת��Ϊ![]() ʱ��
ʱ��![]() ��ֵ�������
��ֵ�������![]() ��
��![]() ��ֵ��Ȼ����зֱ���
��ֵ��Ȼ����зֱ���![]() ��
��![]() ��ֵ�Ӽ��ϼ�İ�����ϵ�������
��ֵ�Ӽ��ϼ�İ�����ϵ�������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�����������1����![]()
��![]() ��
��![]() �ϵ����ݼ�����
�ϵ����ݼ�����![]() ����
����![]() ��
��![]() �ϵ����ݼ���
�ϵ����ݼ���
��![]() ����
����![]() ����
����![]() 4��
4��
��2����![]() ������
������![]() ���Ǽ���������
���Ǽ���������![]() ����
����![]()
��![]() ��
��![]()
��![]() ʱ��
ʱ��![]()
�����������![]() ������
������![]() ��
��
��![]() ����
����![]() ��Ҳ����
��Ҳ����![]()
���Ͽ�֪![]() 8��
8��
��3����![]() ��
��![]() �ϵ�����
�ϵ�����![]() ��
��![]() �ϵݼ���
�ϵݼ���
��![]() ʱ��
ʱ��![]() ��
��![]()
���������![]() ��������
��������![]() ��ʹ��
��ʹ��![]() ����
����
��![]()
![]()
��![]() ������
������![]() 13��
13��

����Ŀ����֪���κ���![]() ����СֵΪ3����
����СֵΪ3����![]() .
.
����![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����ż����![]() ������
������![]() ������ô��
������ô�� ![]() ������
������![]() ���Ƿ������㣿��˵������.
���Ƿ������㣿��˵������.
���𰸡���1��![]() ��2���������
��2���������
�������������������1������ϵ��������֪��������Ϊ���κ�������֪f(-1)=f(3),���ԶԳ�����x=1,�Һ�����Сֵf(1)=3,���躯��![]() ����
����![]() ������f(-1)=11���ɽ�a��
������f(-1)=11���ɽ�a��
��2��������ɵ�![]() ������
������![]() ����
����![]() ���Ĵ����Զ�����
���Ĵ����Զ����� ![]() �����䣨1��2���ϴ�����㡣
�����䣨1��2���ϴ�����㡣
�����������1����Ϊ![]() �Ƕ��κ�������
�Ƕ��κ�������![]()
���Զ��κ���ͼ��ĶԳ���Ϊ![]() ��
��
��![]() ����СֵΪ3�����Կ���
����СֵΪ3�����Կ���![]() ����
����![]()
��![]() ����
����![]()
����![]()
��2���ɣ�1���ɵ�![]() ��
��
��Ϊ![]() ��
��
![]()
����![]() �����䣨1��2���ϴ�����㣮
�����䣨1��2���ϴ�����㣮
���㾦��
��1��������֪���ͺ����ĵĽ���ʽ�����ô���ϵ���������ڶ��κ����ı���ʽ��ʽ�Ƚ϶࣬��һ��ʽ������ʽ������ʽ���ɱ�����������֪���Գ����붥�����꣬�����趥��ʽ��
��2�������ж������ڷ����������⣬һ��������������������ǣ�����ͨ���۲캯��ͼ���ٹ���������ڵ����䣻�ڸ��ݷ��̸��Ĵ����Զ���֤�����Ǵ��ڵģ��������ݺ���������֤������Ψһ��.����������䣬��ֱ���ø��Ĵ����Զ�����
�����͡������
��������
20
����Ŀ�����л�������������˰���涨�������¹��ʡ�н�����ò�����3500Ԫ�IJ��ֲ���˰������3500Ԫ�IJ���Ϊȫ��˰���ö����˰��±��ֶ��ۼƼ��㣺
ȫ��Ӧ��˰���ö� | ˰�� |
������1500Ԫ�IJ��� |
|
����1500Ԫ��4500Ԫ�IJ��� |
|
����4500Ԫ��9000Ԫ�IJ��� |
|
��1����֪���������¹��ʣ�н������Ϊ10000Ԫ����������Ӧ���ɶ��ٸ�������˰��
��2�������������¹��ʣ�н������Ϊ![]() ������Ӧ���ɸ�������˰Ϊ
������Ӧ���ɸ�������˰Ϊ![]() Ԫ��д��
Ԫ��д��![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��3����֪������һ�·�Ӧ���ɸ�������˰Ϊ303Ԫ����ô�����µĹ��ʡ�н������Ϊ���٣�