题目内容
(本小题满分12分)
已知椭圆的中心在坐标原点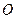 ,焦点在
,焦点在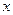 轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,短轴长为2.
轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,短轴长为2.
(1)求椭圆的方程;
(2)设直线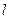 过
过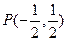 且与椭圆相交于A,B两点,当P是AB的中点时,求直线
且与椭圆相交于A,B两点,当P是AB的中点时,求直线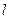 的方程.
的方程.
已知椭圆的中心在坐标原点
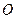 ,焦点在
,焦点在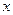 轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,短轴长为2.
轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,短轴长为2.(1)求椭圆的方程;
(2)设直线
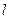 过
过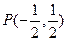 且与椭圆相交于A,B两点,当P是AB的中点时,求直线
且与椭圆相交于A,B两点,当P是AB的中点时,求直线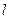 的方程.
的方程.(1)
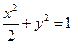
(2)
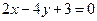
解:设椭圆方程为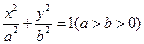 .---
.---
由已知可得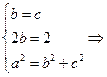
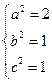
∴所求椭圆方程为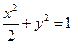 -------------------------------------4分.
-------------------------------------4分.
(Ⅱ)当直线 的斜率存在时,
的斜率存在时,
设直线 的方程为
的方程为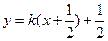 ,
,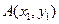 ,
,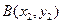 ,
,
则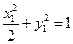 ,
,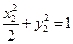 ,
,
两式相减得: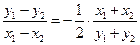 .
.
∵P是AB的中点,
∴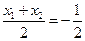 ,
,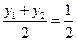 代入上式可得直线AB的斜率为
代入上式可得直线AB的斜率为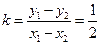 ,
,
∴直线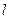 的方程为
的方程为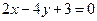 .-----------------------------------------8分
.-----------------------------------------8分
当直线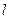 的斜率不存在时,将
的斜率不存在时,将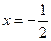 代入椭圆方程并解得
代入椭圆方程并解得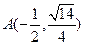 ,
,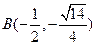 ,这时AB的中点为
,这时AB的中点为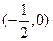 ,
,
∴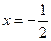 不符合题设要求.----------------------------------10分
不符合题设要求.----------------------------------10分
综上,直线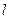 的方程为
的方程为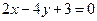 .------------------------- 12分
.------------------------- 12分
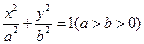 .---
.--- 由已知可得
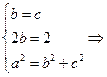
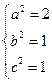
∴所求椭圆方程为
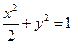 -------------------------------------4分.
-------------------------------------4分. (Ⅱ)当直线
 的斜率存在时,
的斜率存在时,设直线
 的方程为
的方程为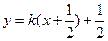 ,
,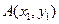 ,
,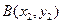 ,
, 则
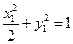 ,
,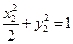 ,
,两式相减得:
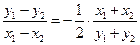 .
. ∵P是AB的中点,
∴
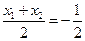 ,
,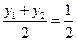 代入上式可得直线AB的斜率为
代入上式可得直线AB的斜率为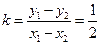 ,
, ∴直线
 的方程为
的方程为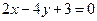 .-----------------------------------------8分
.-----------------------------------------8分当直线
 的斜率不存在时,将
的斜率不存在时,将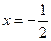 代入椭圆方程并解得
代入椭圆方程并解得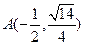 ,
,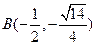 ,这时AB的中点为
,这时AB的中点为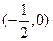 ,
,∴
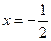 不符合题设要求.----------------------------------10分
不符合题设要求.----------------------------------10分综上,直线
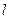 的方程为
的方程为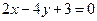 .------------------------- 12分
.------------------------- 12分
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 分)已知椭圆
分)已知椭圆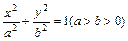 ,直线l与椭圆交于A、B两点,M是线段AB的中点,连接OM并延长交椭圆于点C.直线AB与直线OM的斜率分别为k、m,且
,直线l与椭圆交于A、B两点,M是线段AB的中点,连接OM并延长交椭圆于点C.直线AB与直线OM的斜率分别为k、m,且 .
.
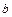 的值;
的值;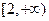 ,使得四边形OACB是平行四边形,请证明你
,使得四边形OACB是平行四边形,请证明你 的结论;
的结论;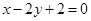 经过椭圆
经过椭圆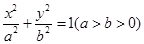 的一个焦点和一个顶点,则该椭圆的离心率为.
的一个焦点和一个顶点,则该椭圆的离心率为.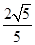
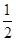
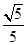
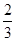
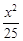 +
+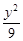 =1上一点P到左焦点F1的距离为2,M是线段PF1的中点,则M到原点O的距离等于( )
=1上一点P到左焦点F1的距离为2,M是线段PF1的中点,则M到原点O的距离等于( )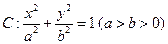 的离心率为
的离心率为 ,长轴端点与短轴端点间的距离为
,长轴端点与短轴端点间的距离为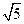 .
.  的方程;
的方程;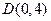 的直线
的直线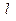 与椭圆
与椭圆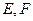 ,
,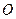 为坐标原点,若
为坐标原点,若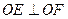 ,求
,求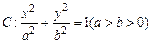 的左焦点为
的左焦点为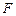 ,过点
,过点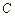 相交于
相交于 两点,直线
两点,直线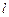 的倾斜角为60o,
的倾斜角为60o,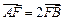 .
.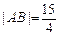 ,求椭圆
,求椭圆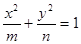 表示焦点在x轴上的椭圆有
表示焦点在x轴上的椭圆有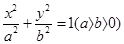 长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,且
长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,且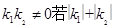 的最小值为1,则椭圆的离心率( )
的最小值为1,则椭圆的离心率( )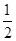 B.
B.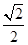 C.
C.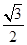 D.
D.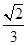
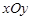 中,已知△
中,已知△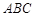 顶点
顶点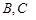
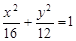 的两个焦点,顶点
的两个焦点,顶点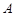 在该椭圆上,则
在该椭圆上,则 =_______________.
=_______________.