题目内容
在平面直角坐标系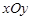 中,已知△
中,已知△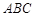 顶点
顶点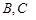
分别为椭圆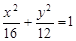 的两个焦点,顶点
的两个焦点,顶点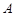 在该椭圆上,则
在该椭圆上,则 =_______________.
=_______________.
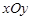 中,已知△
中,已知△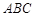 顶点
顶点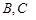
分别为椭圆
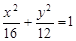 的两个焦点,顶点
的两个焦点,顶点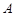 在该椭圆上,则
在该椭圆上,则 =_______________.
=_______________.2
略

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
题目内容
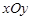 中,已知△
中,已知△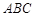 顶点
顶点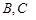
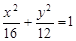 的两个焦点,顶点
的两个焦点,顶点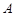 在该椭圆上,则
在该椭圆上,则 =_______________.
=_______________.
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案