题目内容
2.已知a,b∈R,a2-2ab+5b2=4,则ab的最小值为$\frac{1-\sqrt{5}}{2}$.分析 a2-2ab+5b2=4,配方为(a-b)2+(2b)2=4,令a-b=2cosθ,2b=2sinθ,θ∈[0,2π).可得ab=(sinθ+2cosθ)sinθ=$\frac{1}{2}$+$\frac{\sqrt{5}}{2}$sin(2θ-α),即可得出.
解答 解:a2-2ab+5b2=4,配方为(a-b)2+(2b)2=4,
令a-b=2cosθ,2b=2sinθ,θ∈[0,2π).
∴b=sinθ,a=sinθ+2cosθ,
∴ab=(sinθ+2cosθ)sinθ=sin2θ+sin2θ=$sin2θ+\frac{1-cos2θ}{2}$=$\frac{1}{2}$+$\frac{\sqrt{5}}{2}$sin(2θ-α),tanα=$\frac{1}{2}$.
∴当sin(2θ-α)=-1,
ab取得最小值:$\frac{1-\sqrt{5}}{2}$.
故答案为:$\frac{1-\sqrt{5}}{2}$.
点评 本题考查了配方法、三角函数代换法、三角函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
12.为得到函数$y=sin(3x+\frac{π}{4})$的图象,只要把函数$y=sin(x+\frac{π}{4})$图象上所有的点( )
| A. | 横坐标缩短到原来的$\frac{1}{3}$倍,纵坐标不变 | |
| B. | 横坐标伸长到原来的3倍,纵坐标不变 | |
| C. | 纵坐标伸长到原来的3倍,横坐标不变 | |
| D. | 纵坐标缩短到原来的$\frac{1}{3}$倍,横坐标不变 |
13.已知i是虚数单位,若(-1-2i)z=1-i则$\overline z$在复平面上所代表的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.已知向量$\overrightarrow{a}$⊥$\overrightarrow{b}$,|$\overrightarrow{a}$-$\overrightarrow{b}$|=2,定义:$\overrightarrow{{c}_{λ}}$=λ$\overrightarrow{a}$+(1-λ )$\overrightarrow{b}$,其中0≤λ≤1.若$\overrightarrow{{c}_{λ}}$•$\overrightarrow{{c}_{\frac{1}{2}}}$=$\frac{1}{2}$,则|$\overrightarrow{{c}_{λ}}$|的最大值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
7.已知f(x)是定义在R上的奇函数,且当x>0时,f(x)=$\left\{\begin{array}{l}cos\frac{πx}{6},0<x≤8\\ lo{g}_{2}x,x>8\end{array}\right.$,则f(f(-16))=( )
| A. | $-\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
11.已知复数z满足(1-i)z=i2015(其中i为虚数单位),则$\overline{z}$的虚部为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$i | D. | -$\frac{1}{2}$i |
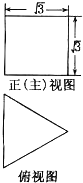 一个底面为正三角形的直三棱柱的正视图和俯视图(单位:cm)如图所示,则它的外接球的表面积等于$\frac{25π}{3}$cm2.
一个底面为正三角形的直三棱柱的正视图和俯视图(单位:cm)如图所示,则它的外接球的表面积等于$\frac{25π}{3}$cm2.