Question

【题目】某企业生产A、B两种产品，生产每一吨产品所需的劳动力和煤、电耗如下表：

产品品种	劳动力	煤吨	电千瓦
A产品	3	9	4
B产品	10	4	5

已知生产每吨A产品的利润是7万元，生产每吨B产品的利润是12万元，现在条件有限，该企业仅有劳动力300个，煤360吨，并且供电局只能供电200千瓦，试问：该企业生产A、B两种产品各多少吨，才能获得最大利润？并求出最大利润．

Answer 1

【答案】该企业生产A，B两种产品分别为20吨和24吨时，才能获得最大利润.

【解析】

试题由题意设生产A，B两种产品分别为x吨，y吨，利润为z万元，则得线性约束条件为

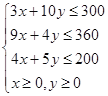
目标函数为z＝7x＋12y.作出可行域，当直线7x＋12y＝0向右上方平行移动时，经过M(20,24)时z取最大值．

试题解析:

设生产A，B两种产品分别为x吨，y吨，利润为z万元，依题意，得

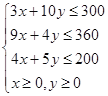
目标函数为z＝7x＋12y.作出可行域，如图阴影所示．当直线7x＋12y＝0向右上方平行移动时，经过M(20,24)时z取最大值．

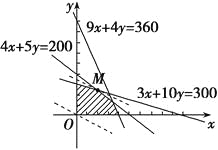
∴该企业生产A，B两种产品分别为20吨和24吨时，才能获得最大利润．