题目内容
2.椭圆E:$\frac{x^2}{5}$+$\frac{y^2}{4}$=1的右焦点F,直线l与曲线x2+y2=4(x>0)相切,且交椭圆E于A,B两点,记△FAB的周长为m,则实数m的所有可能取值所成的集合为{2$\sqrt{5}$}.分析 确定AQ,BQ,利用椭圆第二定义,即可求出实数m的所有可能取值所成的集合
解答 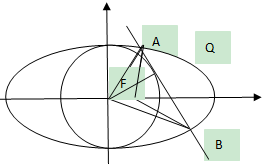 解:设A(x1,y1),B(x2,y2),切点为Q,则
解:设A(x1,y1),B(x2,y2),切点为Q,则
$\begin{array}{l}A{Q^2}=A{O^2}-{r^2}={x^2}_1+{y_1}^2-4(∵\frac{{{x_1}^2}}{5}+\frac{{{y_1}^2}}{4}=1)\\={x^2}_1+4(1-\frac{{{x_1}^2}}{5})-4=\frac{{{x_1}^2}}{5}\\∴AQ=\frac{{{x_1}^{\;}}}{{\sqrt{5}}}(∵{x_1}>0)\end{array}$
同理可求得:$BQ=\frac{{{x_2}^{\;}}}{{\sqrt{5}}}$
由椭圆第二定义:
$\begin{array}{l}AF=a-e{x_1}=\sqrt{5}-\frac{1}{{\sqrt{5}}}{x_1}\\ BF=a-e{x_2}=\sqrt{5}-\frac{1}{{\sqrt{5}}}{x_2}\\ AF+BF=2\sqrt{5}-\frac{1}{{\sqrt{5}}}({x_1}+{x_2})\end{array}$
$\begin{array}{l}△ABF周长=AB+AF+BF=\frac{1}{{\sqrt{5}}}({x_1}+{x_2})+2\sqrt{5}-\frac{1}{{\sqrt{5}}}({x_1}+{x_2})\\=2\sqrt{5}(为定值)\end{array}$
故答案为:{2$\sqrt{5}$}.
点评 本题考查椭圆方程与性质,考查椭圆的定义,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
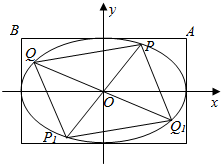 已知椭圆C的中心在原点,左焦点为F1(-1,0),右准线方程为:x=4
已知椭圆C的中心在原点,左焦点为F1(-1,0),右准线方程为:x=4