题目内容
1.已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的长轴长是4,点A为椭圆的右顶点,点B为椭圆上一点,且△OAB是等腰直角三角形(点O为坐标原点).(Ⅰ)求椭圆C的方程;
(Ⅱ)过椭圆C上异于其顶点的任意一点P,作圆x2+y2=$\frac{4}{3}$的两条切线,切点分别为M,N,若直线MN与x,y轴的交点分别是(m,0),(0,n),证明:$\frac{1}{m^2}$+$\frac{3}{n^2}$是定值.
分析 (Ⅰ)由题意求出B的坐标,代入椭圆方程求得b值,则椭圆方程可求;
(Ⅱ)设P(x0,y0)为椭圆$\frac{{x}^{2}}{4}+\frac{3{y}^{2}}{4}=1$上的点,求得${{x}_{0}}^{2}+3{{y}_{0}}^{2}=4$,再求出以OP为直径的圆的方程,和已知圆的方程作差求出两圆公共弦的方程,然后求得m,n的值,代入$\frac{1}{m^2}$+$\frac{3}{n^2}$得答案.
解答 (Ⅰ)解:如图,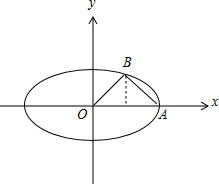 由△OAB是等腰直角三角形,且2a=4,得OA=2,B(1,1),
由△OAB是等腰直角三角形,且2a=4,得OA=2,B(1,1),
代入$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{{b}^{2}}=1$,得$\frac{1}{4}+\frac{1}{{b}^{2}}=1$,∴$\frac{1}{{b}^{2}}=\frac{3}{4}$,
则椭圆方程为$\frac{{x}^{2}}{4}+\frac{3{y}^{2}}{4}=1$;
(Ⅱ)证明:设P(x0,y0)为椭圆$\frac{{x}^{2}}{4}+\frac{3{y}^{2}}{4}=1$上的点,则${{x}_{0}}^{2}+3{{y}_{0}}^{2}=4$,
以OP为直径的圆的方程为$(x-\frac{{x}_{0}}{2})^{2}+(y-\frac{{y}_{0}}{2})^{2}=\frac{{{x}_{0}}^{2}+{{y}_{0}}^{2}}{4}$,
整理得:x2+y2-x0x-y0y=0,①
又圆x2+y2=$\frac{4}{3}$,②
②-①得,直线MN的方程为${x}_{0}x+{y}_{0}y=\frac{4}{3}$,
取y=0,得$x=\frac{4}{3{x}_{0}}$,即m=$\frac{4}{3{x}_{0}}$;
取x=0,得$y=\frac{4}{3{y}_{0}}$,即n=$\frac{4}{3{y}_{0}}$.
∴$\frac{1}{m^2}$+$\frac{3}{n^2}$=$\frac{9}{16}{{x}_{0}}^{2}+\frac{27}{16}{{y}_{0}}^{2}=\frac{9}{16}({{x}_{0}}^{2}+3{{y}_{0}}^{2})=\frac{9}{16}×4=\frac{9}{4}$(为定值).
点评 本题考查了椭圆方程的求法,考查了直线与圆,圆与椭圆的位置关系,关键是求出过点P与圆相切的两切线切点的直线MN的方程,是中档题.

| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{2}{3}$ | D. | $\frac{4}{3}$ |
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
| A. | a>c>b | B. | a>b>c | C. | c>b>a | D. | b>c>a |
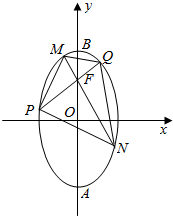 如图所示,椭圆长轴端点为点A、B、O为椭圆的中心,F为椭圆的上焦点,且$\overrightarrow{AF}•\overrightarrow{FB}=1,|\overrightarrow{OF}|=1$.
如图所示,椭圆长轴端点为点A、B、O为椭圆的中心,F为椭圆的上焦点,且$\overrightarrow{AF}•\overrightarrow{FB}=1,|\overrightarrow{OF}|=1$.