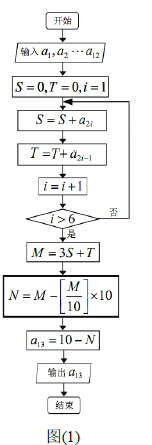
题目内容
【题目】定义![]() 为不超过
为不超过![]() 的最大整数,例如
的最大整数,例如![]() ,
,![]() .已知
.已知![]() 是等比数列,若
是等比数列,若![]() ,且前
,且前![]() 项和为
项和为![]() .
.
(1)若不等式![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)求![]() 的通项公式;
的通项公式;
(3)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)![]() (2)
(2)![]() (3)
(3)
【解析】
(1)首先根据![]() 的范围确定出
的范围确定出![]() 的可能取值有
的可能取值有![]() ,
,![]() ,
,![]() ,分别将
,分别将![]() 取
取![]() ,
,![]() ,
,![]() 代入不等式得到不等式组,求解得结果;
代入不等式得到不等式组,求解得结果;
(2)利用等比数列项之间的关系以及求和公式,得到公比和首项所满足的等量关系式,之后应用等比数列的通项公式求得结果;
(3)根据通项公式写出数列![]() 的若干项,会发现从第五项开始往后都是大于0小于1的数,之后分类讨论求得结果.
的若干项,会发现从第五项开始往后都是大于0小于1的数,之后分类讨论求得结果.
(1)当![]() 时,
时,![]() 的可能取值有
的可能取值有![]() ,
,![]() ,
,![]() ,
,
所以,只需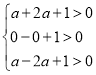 ,解得
,解得![]() ,
,
即实数![]() 的取值范围为
的取值范围为![]() .
.
(2)设等比数列![]() 的公比为
的公比为![]() ,由
,由![]() 可得
可得![]() ,
,
![]() ,由数列的前
,由数列的前![]() 项和为
项和为![]() 可得
可得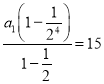 ,解得
,解得![]() .
.
![]() 的通项公式为
的通项公式为 .
.
(3)由已知条件及(2)可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 当
当![]() 时,
时,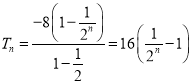
当![]() 时,
时,![]() .
.
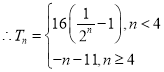 .
.

 阅读快车系列答案
阅读快车系列答案【题目】A市某机构为了调查该市市民对我国申办2034年足球世界杯的态度,随机选取了140位市民进行调查,调查结果统计如下:
支持 | 不支持 | 合计 | |
男性市民 | 60 | ||
女性市民 | 50 | ||
合计 | 70 | 140 |
(1)根据已知数据,把表格数据填写完整;
(2)若在被调查的支持申办足球世界杯的男性市民中有5位退休老人,其中2位是教师,求从这5人中随机抽取3人至多有1人是教师的概率.
【题目】某企业生产![]() 、
、![]() 两种产品,生产每
两种产品,生产每![]() 产品所需的劳动力和煤、电消耗如下表:
产品所需的劳动力和煤、电消耗如下表:
产品品种 | 劳动力(个) | 煤 | 电 |
|
|
|
|
|
|
|
|
已知生产![]() 产品的利润是
产品的利润是![]() 万元,生产
万元,生产![]() 产品的利润是
产品的利润是![]() 万元.现因条件限制,企业仅有劳动力
万元.现因条件限制,企业仅有劳动力![]() 个,煤
个,煤![]() ,并且供电局只能供电
,并且供电局只能供电![]() ,则企业生产
,则企业生产![]() 、
、![]() 两种产品各多少吨,才能获得最大利润?
两种产品各多少吨,才能获得最大利润?
【题目】下表是我省某地区2012年至2018年农村居民家庭年纯收入![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
年纯收入 | 2 | 3 | 3.5 | 4 | 4.5 | 5 | 6 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2012年至2018年该地区农村居民家庭年纯收入的变化情况,并预测该地区2019年农村居民家庭年纯收入(结果精确到0.1)。
附:回归直线的斜率和截距的最小二乘法估计公式分别为: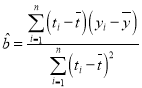 ,
,![]() 。
。