题目内容
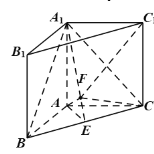
【题目】如图,矩形ABCD和梯形BEFC所在平面互相垂直.,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
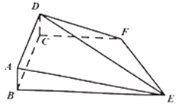
(1)求证:![]() 平面ABE;
平面ABE;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)在BE上取点H,使得![]() ,可得四边形BCFH为矩形,得到
,可得四边形BCFH为矩形,得到![]() ,进一步得到
,进一步得到![]() ,则四边形FDAH为平行四边形,故
,则四边形FDAH为平行四边形,故![]() ,由线面平行的判定可得
,由线面平行的判定可得![]() 平面ABE;
平面ABE;
(2)由平面![]() 平面BEFC结合面面垂直的性质可得
平面BEFC结合面面垂直的性质可得![]() 平面BEFC,过C作
平面BEFC,过C作![]() 交EF的延长线于M,连接DM,可得
交EF的延长线于M,连接DM,可得![]() 为二面角
为二面角![]() 的平面角,然后求解三角形得答案.
的平面角,然后求解三角形得答案.
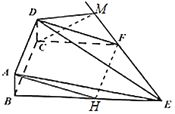
(1)证明:在BE上取点H,使得![]() ,则四边形BCFH为矩形,∴
,则四边形BCFH为矩形,∴![]() ,
,
又![]() ,∴
,∴![]() ,则四边形FDAH为平行四边形,故
,则四边形FDAH为平行四边形,故![]() .
.
∵![]() 平面ABE,
平面ABE,![]() 平面ABE,
平面ABE,
∴![]() 平面ABE;
平面ABE;
(2)解:∵平面![]() 平面BEFC,平面
平面BEFC,平面![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 平面BEFC,
平面BEFC,
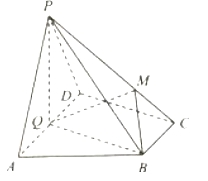
过C作![]() 交EF的延长线于M,连接DM,
交EF的延长线于M,连接DM,
则![]() 为二面角
为二面角![]() 的平面角,
的平面角,
在梯形BCEF中,由![]() ,
,![]() ,可得
,可得![]() ,
,
∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴ .
.
∴ .
.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目