题目内容
【题目】2018年12月18日上午10时，在人民大会堂举行了庆祝改革开放40周年大会．40年众志成城，40年砥砺奋进，40年春风化雨，中国人民用双手书写了国家和民族发展的壮丽史诗．会后，央视媒体平台，收到了来自全国各地的纪念改革开放40年变化的老照片，并从众多照片中抽取了100张照片参加“改革开放40年图片展”，其作者年龄集中在
之间，根据统计结果，做出频率分布直方图如下：
（Ⅰ）求这100位作者年龄的样本平均数
和样本方差
（同一组数据用该区间的中点值作代表）；
（Ⅱ）由频率分布直方图可以认为，作者年龄X服从正态分布
，其中
近似为样本平
均数，
近似为样本方差．
（i）利用该正态分布，求
；
（ii）央视媒体平台从年龄在
和
的作者中，按照分层抽样的方法，抽出了7人参加“纪念改革开放40年图片展”表彰大会，现要从中选出3人作为代表发言，设这3位发言者的年龄落在区间的人数是Y，求变量Y的分布列和数学期望．附：
，若
，则
，
【答案】（1）
,
；（2）（i）0.3415；（ii）详见解析.
【解析】
(1) 利用离散型随机变量的期望与方差的公式计算可得答案；
（2）（i）由(1)知，
)，从而可求出
；
（ii）可得
可能的取值为0，1，2，3，分别求出其概率，可列出的分布列，求出其Y的数学期望.
解：（1）这100位作者年龄的样本平均数
和样本方差
分别为
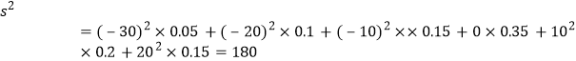
（2）（i）由（1）知，
，
从而
；
（ii）根据分层抽样的原理，可知这7人中年龄在
内有3人，在
内有4人，
故可能的取值为0，1，2，3
，
，
所以的分布列为
Y | 0 | 1 | 2 | 3 |
P |
|
|
|
|
所以Y的数学期望为
练习册系列答案
相关题目
