Question

【题目】在四棱锥P-ABCD中，四边形ABCD是直角梯形,底面,,,是的中点.

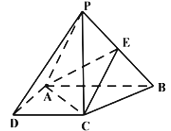
(1)求证：平面平面；

(2)若与平面所成角的正弦值为,求二面角的余弦值.

Answer 1

【答案】(1)证明见解析；(2).

【解析】

(1)在直角梯形ABCD中,利用勾股定理可以证明出,再利用线面垂直的性质定理可以证明出,这样可以利用线面垂直的判定定理、面面垂直的判定定理可以证明出平面平面；

(2)设AB的中点为O,以C为空间直角坐标系原点，以所在的直线分别为轴,写出各点的坐标,根据空间向量数量积公式,通过与平面所成角的正弦值为,可以求出点P的坐标,最后再利用空间向量数量积公式可以求出二面角的余弦值.

(1) 设AB的中点为O,如图所示,因为,所以

,,因为,所以,又因为底面,而底面,所以,

而平面,所以平面,而平面,所以平面平面；

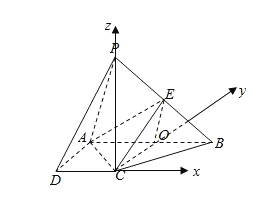
(2) 以C为空间直角坐标系原点，以所在的直线分别为轴,如上图所示：设,因此有：

,

设平面的法向量为：.

,

因为与平面所成角的正弦值为,所以

,所以.

设平面的法向量为,

.

设二面角的平面角为.

.