题目内容
已知元素为正整数的数集序列{1},{2,3},{4,5,6},{7,8,9,10},…从第二个数集开始,每一个数集比前一个数集多一个元素,且每一个数集中最小的元素比前一个数集中最大的元素大1,则第n个数集中所有元素之和Sn= .
考点:数列的求和
专题:计算题,归纳猜想型
分析:由题意知每一个数集的正整数的个数与项数相同,利用等差数列的前n项和公式求出第n-1个数集中最大数,从而确定第n个数集中第一个数,利用等差数列的前n项和公式,求出第n个数集中所有元素之和Sn.
解答:
解:根据题意可知,每一个数集的正整数的个数与项数相同,
所以第n-1个数集中最大数为:1+2+••+n-1=
=
,
则第n个数集中第一个数是
+1=
,
因为每个数集都是以1为公差的等差数列,
所以第n个数集中所有元素之和Sn=
×n+
×1=
,
故答案为:
.
所以第n-1个数集中最大数为:1+2+••+n-1=
| (n-1)(1+n-1) |
| 2 |
| n(n-1) |
| 2 |
则第n个数集中第一个数是
| n(n-1) |
| 2 |
| n2-n+2 |
| 2 |
因为每个数集都是以1为公差的等差数列,
所以第n个数集中所有元素之和Sn=
| n2-n+2 |
| 2 |
| n(n-1) |
| 2 |
| n(n2+1) |
| 2 |
故答案为:
| n(n2+1) |
| 2 |
点评:本题考查等差数列的前n项和公式,以及归纳推理,通过观察个别情况发现其中的规律,以及规律应用.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
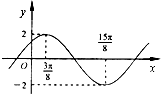 已知函数f(x)=2sin(ωx+ϕ)(ω>0,0<ϕ<π)的图象如图所示,则ω等于( )
已知函数f(x)=2sin(ωx+ϕ)(ω>0,0<ϕ<π)的图象如图所示,则ω等于( )A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
用数字1,2,3,4,5组成无重复数字的五位数,要求1不在首位,3不在百位的五位数共有( )
| A、72 | B、78 | C、96 | D、54 |
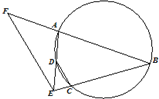 如图,A,B,C,D四点在同一圆上,BC与AD的延长线交于点E,点F在BA的延长线上,若
如图,A,B,C,D四点在同一圆上,BC与AD的延长线交于点E,点F在BA的延长线上,若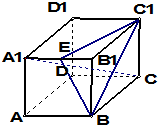 在正方体ABCD-A1B1C1D1中,点E是棱A1B1的中点,
在正方体ABCD-A1B1C1D1中,点E是棱A1B1的中点,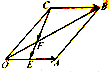 如图,在平行四边形OABC中,E是OA的中点,F在对角线OB上,且OF=
如图,在平行四边形OABC中,E是OA的中点,F在对角线OB上,且OF=