题目内容
 如图,椭圆与双曲线有公共焦点F1、F2,它们在第一象限的交点为A,且AF1⊥AF2,∠AF1F2=30°,则椭圆与双曲线的离心率的倒数和为( )
如图,椭圆与双曲线有公共焦点F1、F2,它们在第一象限的交点为A,且AF1⊥AF2,∠AF1F2=30°,则椭圆与双曲线的离心率的倒数和为( )A、2
| ||
B、
| ||
| C、2 | ||
| D、1 |
考点:双曲线的简单性质,椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:运用椭圆和双曲线的定义,结合离心率公式和解直角三角形的有关知识,化简计算即可得到.
解答:
解:由椭圆的定义,可得,AF1+AF2=2a1,
由双曲线的定义,可得,AF1-AF2=2a2,
在直角△AF1F2中,∠AF1F2=30°,
则AF2=
F1F2=c,AF1=
F1F2=
c,
则有2a1=(
+1)c,2a2=(
-1)c,
则离心率e1=
=
,e2=
=
,
即有
+
=
+
=
.
故选B.
由双曲线的定义,可得,AF1-AF2=2a2,
在直角△AF1F2中,∠AF1F2=30°,
则AF2=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
则有2a1=(
| 3 |
| 3 |
则离心率e1=
| c |
| a1 |
| 2 | ||
|
| c |
| a2 |
| 2 | ||
|
即有
| 1 |
| e1 |
| 1 |
| e2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
故选B.
点评:本题考查椭圆和双曲线的定义和性质:离心率,考查运算能力,属于中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
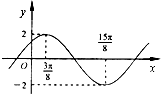 已知函数f(x)=2sin(ωx+ϕ)(ω>0,0<ϕ<π)的图象如图所示,则ω等于( )
已知函数f(x)=2sin(ωx+ϕ)(ω>0,0<ϕ<π)的图象如图所示,则ω等于( )A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
设f(x)=xlnx,若f′(x0)=2,则x0等于( )
| A、e2 | ||
| B、e | ||
C、
| ||
| D、ln2 |
在平面直角坐标系中,不等式组
,(a是常数)表示的平面区域面积是9,那么实数a的值为( )
|
A、3
| ||
B、-3
| ||
| C、-5 | ||
| D、1 |
 已知等差数列{an}的公差为d,前n项和为Sn,且满足
已知等差数列{an}的公差为d,前n项和为Sn,且满足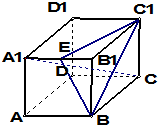 在正方体ABCD-A1B1C1D1中,点E是棱A1B1的中点,
在正方体ABCD-A1B1C1D1中,点E是棱A1B1的中点,