题目内容
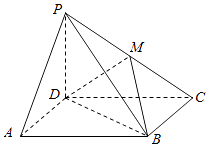
【题目】如图,在空间几何体A﹣BCDE中,底面BCDE是梯形,且CD∥BE,CD=2BE=4,∠CDE=60°,△ADE是边长为2的等边三角形,F为AC的中点. (Ⅰ)求证:BF∥平面ADE;
(Ⅱ)若AC=4,求证:平面ADE⊥平面BCDE;
(Ⅲ)若AC=4,求几何体C﹣BDF的体积.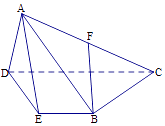
【答案】证明:(Ⅰ)取DA的中点G连结FG,GE, 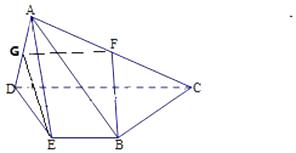
∵F为AC的中点,∴ ![]() ,
,
又∵DC∥BE,CD=2BE,∴EB∥GF,且EB=GF,
∴四边形BFGE为平行四边形,∴BF∥EG,
∵EG平面ADE,BF平面ADE,
∴BF∥平面ADE
解:(Ⅱ)取DE的中点H,连AH,CH,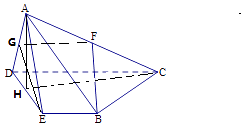
∵△ADE为等边三角形,∴AH⊥DE,且 ![]() ,
,
在△DHC中,DH=1,DC=4,HDC=60°,∴ ![]() ,
,
∴AC2=AH2+HC2 , 即AH⊥HC,∵DE∩HC=H,
∴AH⊥平面BCDE,∵AH平面ADE,
∴平面ADE⊥BCDE…(8分)
(Ⅲ) ![]() =
= ![]() =2,
=2,
∵F是AC中点,
∴几何体C﹣BDF的体积 ![]()
【解析】(Ⅰ)取DA的中点G连结FG,GE,推导出四边形BFGE为平行四边形,从而BF∥EG,由此能证明BF∥平面ADE.(Ⅱ)取DE的中点H,连AH,CH,推导出AH⊥DE,AH⊥HC,从而AH⊥平面BCDE,由此能证明平面ADE⊥BCDE.(Ⅲ)几何体C﹣BDF的体积 ![]() ,由此能求出结果.
,由此能求出结果.
【考点精析】掌握平面与平面垂直的判定是解答本题的根本,需要知道一个平面过另一个平面的垂线,则这两个平面垂直.

练习册系列答案
相关题目