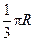题目内容
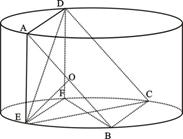
如图所示,圆柱的高为2,底面半径为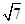 ,AE、DF是圆柱的两条母线,过
,AE、DF是圆柱的两条母线,过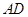 作圆柱的截面交下底面于
作圆柱的截面交下底面于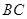 ,四边形ABCD是正方形.
,四边形ABCD是正方形.
(Ⅰ)求证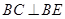 ;
;
(Ⅱ)求四棱锥E-ABCD的体积.
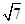 ,AE、DF是圆柱的两条母线,过
,AE、DF是圆柱的两条母线,过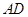 作圆柱的截面交下底面于
作圆柱的截面交下底面于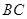 ,四边形ABCD是正方形.
,四边形ABCD是正方形.
(Ⅰ)求证
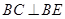 ;
;(Ⅱ)求四棱锥E-ABCD的体积.
(Ⅰ)详见解析;(Ⅱ)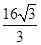
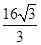
试题分析:(Ⅰ)根据AE是圆柱的母线,所以
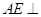 下底面,又
下底面,又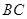
 下底面,则
下底面,则
又截面ABCD是正方形,所以
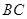 ⊥
⊥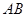 ,又
,又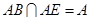
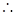
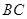 ⊥面
⊥面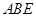 ,又
,又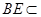 面
面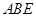 ,即可得到BC⊥BE;
,即可得到BC⊥BE;(Ⅱ)根据锥体的体积公式即可求四棱锥E-ABCD的体积.
试题解析:(Ⅰ)
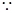 AE是圆柱的母线,
AE是圆柱的母线,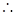
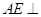 下底面,又
下底面,又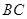
 下底面,
下底面,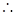
 .3分
.3分又
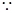 截面ABCD是正方形,所以
截面ABCD是正方形,所以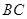 ⊥
⊥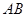 ,又
,又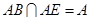
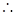
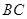 ⊥面
⊥面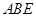 ,又
,又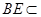 面
面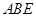 ,
,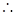
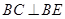 (7分)
(7分)(Ⅱ)因为母线
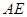 垂直于底面,所以
垂直于底面,所以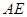 是三棱锥
是三棱锥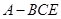 的高 (8分),
的高 (8分),由(Ⅰ)知
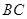 ⊥面
⊥面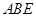 ,
,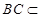 面
面 ,
,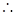 面
面 ⊥面
⊥面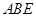 ,
,又
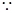 面
面
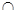 面
面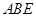
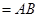 ,
,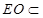 面
面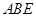 ,
,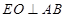
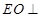 面
面 ,即EO就是四棱锥
,即EO就是四棱锥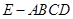 的高 (10分)
的高 (10分)设正方形
 的边长为
的边长为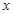 , 则
, 则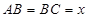 ,
,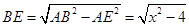
又
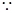
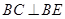 ,
,

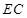 为直径,即
为直径,即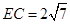
在
 中,
中,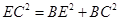 , 即
, 即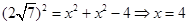
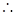
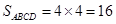 , (12分)
, (12分)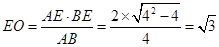
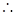
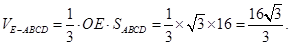

练习册系列答案
相关题目
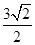 ,底面边长为
,底面边长为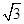 ,则以O为球心,OA为半径的球的表面积为________.
,则以O为球心,OA为半径的球的表面积为________. ,M,N分别是SC,BC的中点,且
,M,N分别是SC,BC的中点,且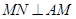 ,则此三棱锥侧棱SA=( )
,则此三棱锥侧棱SA=( )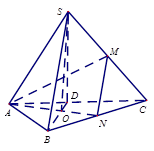


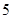
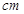 ,侧面积为
,侧面积为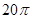
 ,则此圆锥的体积为________
,则此圆锥的体积为________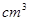 .
.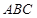 的三个顶点都在半径为
的三个顶点都在半径为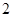 的球面上,球心
的球面上,球心 到平面
到平面 ,点
,点 是线段
是线段 的中点,过
的中点,过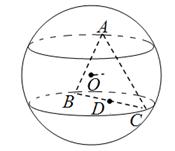

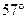 线上,纬度分别为北纬
线上,纬度分别为北纬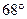 和
和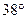 的两地A,B的球面距离为( )
的两地A,B的球面距离为( )