题目内容
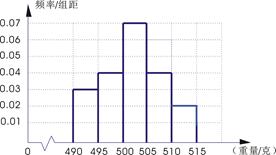
某食品厂为了检查甲乙两条自动包装流水线的生产情况,随即在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在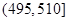 的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.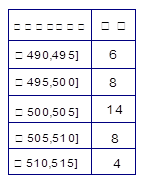
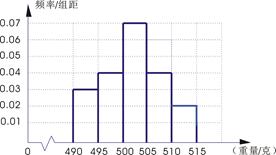
表1:(甲流水线样本频数分布表) 图1:(乙流水线样本频率分布直方图)
(1)根据上表数据在答题卡上作出甲流水线样本的频率分布直方图;
(2)若以频率作为概率,试估计从两条流水线分别任取1件产品,该产品恰好是合格品的概率分别是多少;
(3)由以上统计数据完成下面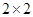 列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
| | 甲流水线 | 乙流水线 | 合计 |
| 合格品 | 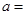 | 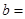 | |
| 不合格品 | 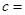 | 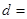 | |
| 合 计 | | |  |
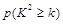 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
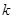 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
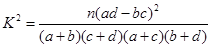 ,其中
,其中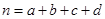 )
)
(1)
(2)甲样本合格品的频率为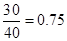
乙样本合格品的频率为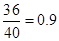 ,
,
(3)90%的把握认为产品的包装质量与两条自动包装流水线的选择有关
解析试题分析:(1)甲流水线样本的频率分布直方图如下: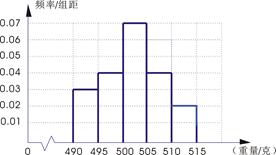
6分
(2)由表1知甲样本中合格品数为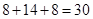 ,由图1知乙样本中合格品数为
,由图1知乙样本中合格品数为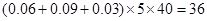 ,故甲样本合格品的频率为
,故甲样本合格品的频率为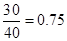
乙样本合格品的频率为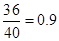 ,
,
据此可估计从甲流水线任取1件产品,该产品恰好是合格品的概率为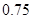
从乙流水线任取1件产品,该产品恰好是合格品的概率为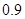 . 8分
. 8分
(3)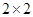 列联表如下:
列联表如下:
12分 甲流水线 乙流水线 合计 合格品 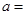 30
30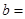 36
3666 不合格品 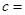 10
10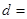 4
414 合 计 40 40  80
80
∵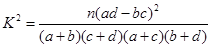 =
=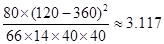
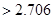
∴有90%的把握认为产品的包装质量与两条自动包装流水线的选择有关. 14分
考点:直方图,独立性检验
点评:解决的关键是根据直方图的概念和独立性检验的公式来得到,属于基础题。

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案设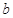 和
和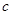 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量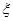 表示方程
表示方程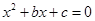 实根的个数(重根按一个计).
实根的个数(重根按一个计).
(1)求方程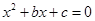 有实根的概率;
有实根的概率;
(2)求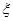 的分布列和数学期望;
的分布列和数学期望;
(3)求在先后两次出现的点数中有5的条件下,方程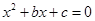 有实根的概率.
有实根的概率.
在某校高三学生的数学校本课程选课过程中,规定每位同学只能选一个科目。已知某班第一小组与第二小组各 有六位同学选择科目甲或科 目乙,情况如下表:
| | 科目甲 | 科目乙 | 总计 |
| 第一小组 | 1 | 5 | 6 |
| 第二小组 | 2 | 4 | 6 |
| 总计 | 3 | 9 | 12 |
(1)求选出的4 人均选科目乙的概率;
(2)设
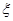 为选出的4个人中选科目甲的人数,求
为选出的4个人中选科目甲的人数,求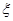 的分布列和数学期望.
的分布列和数学期望. 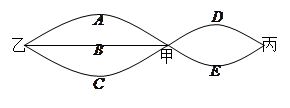
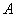 、
、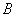 、
、 上下班时间往返出现拥堵的概率都是
上下班时间往返出现拥堵的概率都是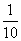 ,
, 、
、 上下班时间往返出现拥堵的概率都是
上下班时间往返出现拥堵的概率都是 ,只要遇到拥堵上学和上班的都会迟到.
,只要遇到拥堵上学和上班的都会迟到.
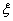 表示李生下班时从单位乙到达小学丙遇到拥堵的次数,求
表示李生下班时从单位乙到达小学丙遇到拥堵的次数,求 ,不堵车的概率为
,不堵车的概率为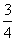 ;汽车走二号公路堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走一号公路,丙汽车由于其他原因走二号公路,且三辆车是否堵车相互之间没有影响.
;汽车走二号公路堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走一号公路,丙汽车由于其他原因走二号公路,且三辆车是否堵车相互之间没有影响.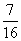 ,求走二号公路堵车的概率;
,求走二号公路堵车的概率;
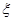 表示抽到“极幸福”的人数, 求
表示抽到“极幸福”的人数, 求 为检测出不合格产品的听数,求
为检测出不合格产品的听数,求