题目内容
市民李生居住在甲地,工作在乙地,他的小孩就读的小学在丙地,三地之间的道路情
况如图所示.假设工作日不走其它道路,只在图示的道路中往返,每次在路口选择道路是随机
的.同一条道路去程与回程是否堵车相互独立. 假设李生早上需要先开车送小孩去丙地小学,
再返回经甲地赶去乙地上班.假设道路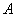 、
、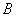 、
、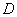 上下班时间往返出现拥堵的概率都是
上下班时间往返出现拥堵的概率都是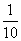 ,
,
道路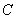 、
、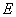 上下班时间往返出现拥堵的概率都是
上下班时间往返出现拥堵的概率都是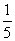 ,只要遇到拥堵上学和上班的都会迟到.
,只要遇到拥堵上学和上班的都会迟到.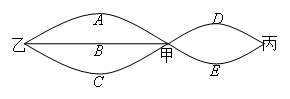
(1)求李生小孩按时到校的概率;
(2)李生是否有八成把握能够按时上班?
(3)设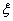 表示李生下班时从单位乙到达小学丙遇到拥堵的次数,求
表示李生下班时从单位乙到达小学丙遇到拥堵的次数,求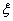 的均值.
的均值.
(1) (2)李生没有八成把握能够按时上班(3)
(2)李生没有八成把握能够按时上班(3)
解析试题分析:⑴因为道路D、E上班时间往返出现拥堵的概率分别是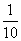 和
和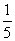 ,
,
因此从甲到丙遇到拥堵的概率是
所以李生小孩能够按时到校的概率是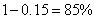 ;
;
⑵甲到丙没有遇到拥堵的概率是 ,
,
丙到甲没有遇到拥堵的概率也是 ,
,
甲到乙遇到拥堵的概率是 ,
,
甲到乙没有遇到拥堵的概率是 ,李生上班途中均没有遇到拥堵的概率是
,李生上班途中均没有遇到拥堵的概率是 ,所以李生没有八成把握能够按时上班
,所以李生没有八成把握能够按时上班
⑶依题意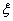 可以取
可以取 .
.  =
=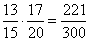 ,
,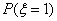 =
= ,
,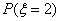 =
= ,
,
分布列是: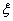
0 1 2 
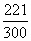


 .
.
考点:随机事件概率
点评:本题着重考查了用树状图列举随机事件出现的所有情况,并求出某些事件的概率,但
应注意在求概率时各种情况出现的可能性务必相同.用到的知识点为:概率=所求情况数与
总情况数之比.

生产A,B两种元件,其质量按测试指标划分为:指标大于或等于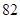 为正品,小于
为正品,小于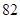 为次品.现随机抽取这两种元件各
为次品.现随机抽取这两种元件各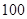 件进行检测,检测结果统计如下:
件进行检测,检测结果统计如下:
| 测试指标 |  | 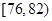 | 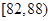 | 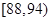 | 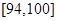 |
| 元件A | 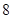 | 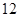 | 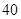 | 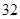 | 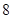 |
| 元件B | 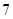 | 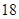 | 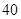 | 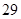 | 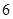 |
(Ⅱ)生产一件元件A,若是正品可盈利40元,若是次品则亏损5元;生产一件元件B,若是正品可盈利50元,若是次品则亏损10元.在(Ⅰ)的前提下,
(ⅰ)记
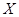 为生产1件元件A和1件元件B所得的总利润,求随机变量
为生产1件元件A和1件元件B所得的总利润,求随机变量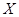 的分布列和数学期望;
的分布列和数学期望;(ⅱ)求生产5件元件B所获得的利润不少于140元的概率.
某食品厂为了检查甲乙两条自动包装流水线的生产情况,随即在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在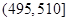 的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.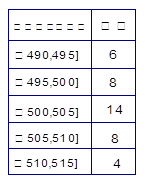
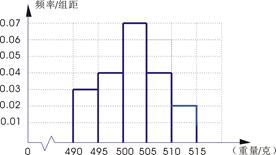
表1:(甲流水线样本频数分布表) 图1:(乙流水线样本频率分布直方图)
(1)根据上表数据在答题卡上作出甲流水线样本的频率分布直方图;
(2)若以频率作为概率,试估计从两条流水线分别任取1件产品,该产品恰好是合格品的概率分别是多少;
(3)由以上统计数据完成下面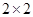 列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
| | 甲流水线 | 乙流水线 | 合计 |
| 合格品 | 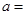 | 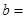 | |
| 不合格品 | 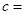 | 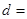 | |
| 合 计 | | | 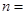 |
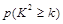 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
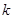 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
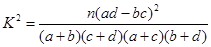 ,其中
,其中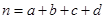 )
)
 ,求
,求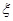 ,求随机变量
,求随机变量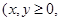 且
且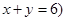 ,乙箱中只放有2个红球、1个白球与1个黑球(球除颜色外,无其它区别). 若甲箱从中任取2个球, 从乙箱中任取1个球.
,乙箱中只放有2个红球、1个白球与1个黑球(球除颜色外,无其它区别). 若甲箱从中任取2个球, 从乙箱中任取1个球.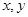 的值;
的值;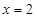 时,求取出的3个球中红球个数
时,求取出的3个球中红球个数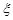 的期望
的期望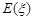 .
. ,且每题正确完成与否互不影响。试从至少正确完成2题的概率分析比较两位考生的实验操作能力.
,且每题正确完成与否互不影响。试从至少正确完成2题的概率分析比较两位考生的实验操作能力.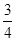 ,甲、丙二人都回答错的概率是
,甲、丙二人都回答错的概率是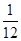 ,乙、丙二人都回答对的概率是
,乙、丙二人都回答对的概率是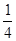 .
.