题目内容
20.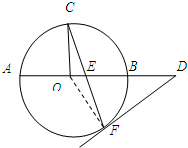 如图,AB是⊙O的直径,C,F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连结CF交AB于点E,OA=3,DB=3,则DE=3$\sqrt{3}$.
如图,AB是⊙O的直径,C,F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连结CF交AB于点E,OA=3,DB=3,则DE=3$\sqrt{3}$.
分析 连接OF,利用切线的性质及角之间的互余关系得到DF=DE,再结合切割线定理证明DE2=DB•DA,即可求出DE.
解答 解:连结OF.
∵DF切⊙O于F,∴∠OFD=90°,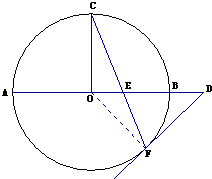
∴∠OFC+∠CFD=90°.
∵OC=OF,
∴∠OCF=∠OFC.
∵CO⊥AB于O,
∴∠OCF+∠CEO=90°.
∴∠CFD=∠CEO=∠DEF,
∴DF=DE.
∵DF是⊙O的切线,∴DF2=DB•DA.
∴DE2=DB•DA,
∵OA=3,DB=3,
∴DE2=DB•DA=3×9=27,
∴DE=3$\sqrt{3}$.
故答案为:3$\sqrt{3}$.
点评 本题主要考查了与圆有关的比例线段、圆的切线的性质定理的应用,属于基础题之列.

练习册系列答案
相关题目
8.已知角θ的终边经过点P(4,m),且sinθ=$\frac{3}{5}$,则m等于( )
| A. | -3 | B. | 3 | C. | $\frac{16}{3}$ | D. | ±3 |
15.已知集合A={x|x2-2x-3<0},Z为整数集,则集合A∩Z中所有元素的和为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.将函数y=sin2x的图象向左平移φ(0<φ<π)个单位后得函数$y=sin({2x-\frac{π}{3}})$的图象,则φ的值为( )
| A. | $\frac{π}{3}$ | B. | $\frac{5π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{6}$ |
12.在寒假来临之际,小赵计划利用寒假进行一次打工体验,已知小赵在某工厂打工,老板告之每天的上班时间(单位:小时)和工资(单位:元),如表所示:
如果根据计算,小赵得知这段时间每天打工工资与每天工作时间满足的线性回归方程为$\stackrel{∧}{y}$=11.4x+5.9,则由此可知老板规定的每天工作12小时可以获得的工资为( )
| 时间x/小时 | 2 | 3 | 5 | 8 | 9 | 12 |
| 工资y/元 | 30 | 40 | 60 | 90 | 120 | m |
| A. | 125元 | B. | 128元 | C. | 140元 | D. | 142.7元 |
10.已知数列{an}的首项为a1=1,且满足对任意的n∈N*,都有an+1-an=2n成立,则a2015=( )
| A. | 22014-1 | B. | 22015-1 | C. | 22015+1 | D. | 22016-1 |