题目内容
10.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左焦点F1坐标为$({-2\sqrt{2},0})$,且椭圆C的短轴长为4,斜率为1的直线l与椭圆G交于A,B两点,以AB为底边的等腰三角形,顶点为P(-3,2)(1)求椭圆C的方程
(2)求△PAB的面积.
分析 (1)通过左焦点坐标可得$c=2\sqrt{2}$,通过椭圆C的短轴长为4可得b=2,进而可得结论;
(2)通过设直线l的方程为y=x+m,并与椭圆方程联立,利用韦达定理可用m表示出|AB|、|PE|,利用PA=PB,E为AB的中点可得PE⊥AB,即可解得m=2,进而计算可得结论.
解答 解:(1)∵左焦点F1坐标为$({-2\sqrt{2},0})$,∴$c=2\sqrt{2}$,
∵椭圆C的短轴长为4,∴2b=4,即b=2,
∴a2=b2+c2=12,
∴椭圆C方程为:$\frac{x^2}{12}+\frac{y^2}{4}=1$;
(2)设直线l的方程为:y=x+m,
由$\left\{\begin{array}{l}y=x+m\\ \frac{x^2}{12}+\frac{y^2}{4}=1\end{array}\right.$,消去y整理得:4x2+6mx+3m2-12=0,
设A,B的坐标分别为(x1,y1),(x2,y2),AB的中点为E(x0,y0),
则${x_0}=\frac{{{x_1}+{x_2}}}{2}=-\frac{3m}{4}$,${x_1}{x_2}=\frac{{3{m^2}-12}}{4}$,${y_0}={x_0}+m=\frac{m}{4}$,
又PA=PB,E为AB的中点,∴PE⊥AB,
∴${k_{PE}}=\frac{{2-\frac{m}{4}}}{{-3+\frac{3m}{4}}}=-1$,解得m=2,
∴$|{AB}|=\sqrt{1+{k^2}}\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}=3\sqrt{2}$,
$|{PE}|=\sqrt{{{(-3+\frac{3}{2})}^2}+{{(2-\frac{1}{2})}^2}}=\frac{{3\sqrt{2}}}{2}$,
∴△PAB的面积$S=\frac{1}{2}|{AB}|•|{PE}|=\frac{9}{2}$.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.

| A. | ∅ | B. | {x|$\frac{1}{2}$<x≤1} | C. | {x|x<1} | D. | {x|0<x<1} |
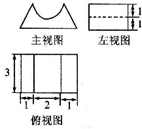
| A. | 27-$\frac{3π}{2}$ | B. | 18-$\frac{3π}{2}$ | C. | 27-3π | D. | 18-3π |
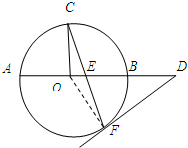 如图,AB是⊙O的直径,C,F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连结CF交AB于点E,OA=3,DB=3,则DE=3$\sqrt{3}$.
如图,AB是⊙O的直径,C,F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连结CF交AB于点E,OA=3,DB=3,则DE=3$\sqrt{3}$.